發展歷程,介質影響,質能方程推導,相關理論,研究歷史,研究方法,天文學方法,羅默的衛星蝕法,布萊德雷的光行差法,地面測量方法,伽利略測定光速的方法,旋轉齒輪法,旋轉稜鏡法,實驗室方法,微波諧振腔法,雷射測速法,實驗論證,
發展歷程 真空中的光速(speed of light/ velocity of light)是自然界物體運動的最大速度。光速與觀測者相對於光源的運動速度無關。物體的質量將隨著速度的增大而增大,當物體的速度接近光速時,它的
動質量 將趨於無窮大,所以質量不為0的物體達到光速是不可能的。只有靜質量為零的光子,才始終以光速運動著。光速與任何速度疊加,得到的仍然是光速。真空中的光速是一個重要的物理常量。
光速 真空光速定義值:c0 =299792458m/s
光速計算值:c0 =299792.458km/s (一般取300000km/s)
作用:當某物體
運動速度 相對於另一物體接近光速,某物體的時間相對於另一物體減慢,時間變化符合
洛倫茲變換 。(二十世紀七十年代通過衛星和地面天文台觀測日食的同一時間位置的不同得以證實)光速是目前已知的最大速度,物體達到光速時
動能 無窮大,所以按當前人類的認知來說達到光速不可能,所以光速、
超光速 的問題不在物理學討論範圍之內。
自20世紀初起,我們的理論一直受制於
愛因斯坦 驗證的光速極限,即每秒186282英里(約合每秒30萬公里)。即使我們把宇宙飛船加速到這一速度,到達距離我們最近的恆星系統半人馬座阿爾法星(距離我們大約4.3
光年 )並返回,也需要近十年時間。此外,宇宙飛船本身還要考慮能量限制。因此,必須要實現突破
光速極限 才有可能實現這些目的。科學家們實施了許多相關的實驗,比如由美國普林斯頓大學科學家王利軍(Lijun Wang)於2000年進行的實驗和德國科學家於2007年進行的實驗都取得了一定的進展。最初,科學家們堅信沒有任何物質或信息能夠突破光速,但光脈衝卻能夠做到。在真空狀態下,在不同位置測到的光脈衝似乎以一種難以置信的速度在傳播。不過,這一速度仍然無法對我們太空旅行提供太大的幫助。2007年的實驗仍然存在爭議。
貝勒大學物理學教授傑拉德-克利弗爾認為,在“
量子糾纏 ”現象中,信息的傳播速度似乎比光速快。2007年和2008年的兩次實驗表明,“
量子糾纏 ”的速度至少是光速的1萬倍。未來實現超光速的方法可能是跳躍到
多維空間 中。美國宇航局突破推進物理學計畫前負責人馬克-米利斯現致力於研究星際旅行,他表示,“肯定還有我們沒發現的物理學領域。”米利斯舉例指出,
暗物質 和
暗能量 或許能夠為我們帶來曙光。
真空中的光速等於299,792,458米/秒(1,079,252,848.88千米/小時)。[2]這個速度並不是一個測量值,而是一個定義。它的計算值為(299792500±100)米/秒。
國際單位制 的基本單位米於1983年10月21日起被定義為光在1/299,792,458秒內傳播的距離。使用
英制單位 ,光速約為186,282.397英里/秒,或者670,616,629.384
英里 /小時,約為1英尺/
納秒 。
在任何透明或者半透明的介質(比如
玻璃 和
水 )中,光速會降低;光在真空中的速度和光在某種介質中的速度之比就是這種介質的
折射率 。
重力 的改變能夠彎曲光所傳播的空間,使光像通過凸透鏡一樣發生彎曲,看上去繞過了質量較大的天體。光彎曲的現象叫做
引力透鏡效應 ,根據變化了的光線在光譜外波段呈現的不規則程度,可以推算發光星系的年齡和距離。
2011年9月22日,義大利物理學家在OPERA實驗中發現了一種超出光速40322.58分之一的
中微子 ,如果實驗數據確鑿無誤,
愛因斯坦 的相對論將會受到挑戰。但是隨後便發現,該實驗結果為設備線路接錯而造成。該實驗結果於2012年6月8日被該小組宣布撤銷。根據愛因斯坦的相對論,沒有任何物體或信息運動的速度可以超過真空中的光速(c)。
介質影響 令
,
且設
v 是靜止介質中的光速,
u 是介質的運動速度,
v '是所要求得的運動介質中的光速。另請不要在意下文
矢量 的書寫
光在不同介質中的速度不同,由於光是
電磁波 ,因此光速也就依賴於介質的介電常數和磁導率。在
各向同性 的靜止介質中,光速是一個小於真空光速c的定值。如果介質以一定的速度運動,則一般求光速的方法是先建立一個隨動參考系,其中的光速是靜止介質中的光速,然後通過參考系變換得到運動介質中的光速;或者可以直接用相對論速度疊加公式去求運動介質中的光速。
光和聲雖然都具有波動性質,但兩者
波速 的算法是完全不同的。以聲音實驗為例:空氣對地面靜止,第1次我們不動測得我們發出的聲音1秒鐘前進了300米;第二次我們1秒鐘勻速後退1米,測得聲音距我們301米,得到結論:兩次聲音相對地面速度不變,相對我們,第一次300米/秒;第2次301米/秒。在牽涉到的速度遠小於光速的情況下,聲速滿足線性疊加。
換做光實驗,我們用玻璃
介質 再做一次,靜止玻璃中的光速,在各個方向上都是相等的。我們再做一個我們不動,讓玻璃勻速運動的實驗,會發現光對玻璃的速度在不同方向上是不等的,但不是簡簡單單的線性疊加了,而是遵循相對論速度疊加:
其實在前述聲速實驗中,聲速嚴格來講遵循的也是
相對論 速度疊加,只是若u、v都遠小於光速c,則式子中
是個很小的值,近似略去之後就得
v'≈v+u ,回到經典的線性疊加形式。
所以,千萬不可以用低速條件下機械波的近似規律去硬套光波。作為狹義相對論基本假設之一的
光速不變原理 ,永遠指的是
真空 中的光速c不變,它是基本物理常數之一。如果有介質,就需要利用相對論速度疊加公式去求光速,切忌用簡單線性疊加。對光速不變原理的正確理解,是正確理解狹義相對論的關鍵之一。
不同介質中有不同的光速值。1850年菲佐用齒輪法測定了光在水中的速度,證明水中光速小於空氣中的光速。幾乎在同時,傅科用旋轉鏡法也測量了水中的光速(
),得到了同樣結論。這一實驗結果與
波動說 相一致而與
牛頓 的微粒說相矛盾(解釋
光的折射定律 時),這對光的波動本性的確立在歷史上曾起過重要作用。1851年,菲佐用干涉法測量了運動介質中的光速,證實了A.-J.菲涅耳的曳引公式。[玻璃中光速
]
質能方程推導 第一步:要討論能量隨質量變化,先要從量綱得知思路。
能量量綱
,即能量量綱等於質量量綱和長度量綱的平方以及時間量綱的負二次方三者乘積。
我們需要把能量對於質量的函式形式化簡到最簡,那么就要求能量函式中除了質量,最好只有一個其它的變數。
把
化簡,可以得到只有一個量綱-速度量綱[V]的形式:[V]×[V]。
也就是[E]=[M][V]×[V]
可見我們要討論質能關係,最簡單的途徑是從速度下手。
第二步:先要考慮能量的變化 與能量的變化有關的有各種能量形式的轉化,其中直接和質量有關的只有做功。
那么先來考慮做功對於能量變化的影響。
當外力
作用在
靜止質量 為m0的質點上時,每產生
的位移,物體能量增加:
考慮最簡化的 外力與位移方向相同的情況,上式變成:
第三步:怎樣把力做功和速度v變化聯繫起來呢?也就是說怎樣來通過
力的作用效果 來得出速度的變化呢?
我們知道力對物體的衝量等於物體
動量 的增量。那么,通過
動量定理 ,力和能量就聯繫起來了:
第四步:上式中顯然還要參考m質量這個變數,而我們不想讓質量的加入把我們力和速度的關係複雜化。我們想找到一種辦法約掉m,這樣就能得到純粹的速度和力的關係。
那么可以得到:
如果考慮最簡單的形式:當速度改變和動量改變方向相同:
dE=vdP
第五步:把上式化成能量和質量以及速度三者的關係式(因為我們最初就是要討論這個形式):
∵dP=d(mv) ,∴dE=vd(mv)
第六步:把上式按照微分乘法分解:
這個式子說明:能量的增量含有質量因速度的增加而增加(量為
dm )所產生的能量增量和單純速度增加產生的能量增量2個部分。(這個觀點非常重要,在相對論之前,人們雖然在
理論物理 推導中認識到質量增加也會產生能量增量,但是都習慣性認為質量不會隨運動速度增加而變化,也就是誤以為
dm 恆定為0,這是
經典物理學 的最大錯誤之一。)
第七步:我們不知道質量隨速度增加產生的增量dm 是怎樣的,要研究它到底如何隨速度增加(也就是質量增量dm 和速度增量dv 之間的直接關係):
根據
洛侖茲變換 推導出的靜止質量
和運動質量
m 公式:
化簡成整數次冪形式:
化成沒有分母而且
m 和
分別處於等號兩側的形式(這樣就是得到運動質量
m 對於速度變化和靜止質量的純粹的函式形式):
用上式對速度
v 求導得到
(之所以要這樣做,就是要找到質量增量dm和速度增量dv之間最直接的關係,我們這一步的根本目的就是這個):
即:
即:
即:
約掉公因式2m (肯定不是0,呵呵,運動質量為0?沒聽說過)
得到:
即:
由於dv 不等於0(我們研究的就是非靜止的情況,運動系速度對於靜止系的增量當然不為0),
這就是我們最終得到的dm 和dv 的直接關係。
第八步:有了dm 的函式,代回到我們第六步的能量增量式:
這就是質能關係式的微分形式,它說明:質量的增量與能量的增量成正比,而且比例係數是常數
最後一步:推論出物體從靜止到運動速度為v 的過程中,總的能量增量:
對上一步的結論進行積分,積分區間取質量從靜止質量
到運動質量
m ,得到:
即:
這就是 物體從靜止到運動速度為v 的過程中,總的能量增量。
其中:
稱為物體運動時候的總動能(運動總能量),此時請注意
m 為運動狀態物體的相對論質量。
總結:對於任何已知運動質量為
m 的物體,可以用
直接計算出它的運動動能。
相關理論 在20世紀愛因斯坦狹義相對論中
質能等價理論 的推論,即著名的方程式
,式(
質能方程 )中為E能量,單位電子伏特(eV),m為質量,c為光速;也就是說,一切物質都潛藏著質量乘以光速平方的能量。一個靜止的物體,其全部的能量都包含在靜止的質量中。一旦運動,就要產生
動能 。由於
質量和能量 等價,運動中所具有的能量應加到質量上,也就是說,運動的
物體的質量 會增加。當物體的運動速度遠低於光速時,增加的質量微乎其微,如速度達到光速的10%時,質量只增加0.5%。但隨著速度接近光速,其增加的質量就顯著了。如速度達到光速的86.6%時,其質量增加了一倍。這時,物體繼續加速就需要更多的能量。當速度趨近光速時,質量隨著速度的增加而成幾何倍數上升,速度無限接近光速時,質量趨向於無限大,需要無限多的能量。因此,任何物體的運動速度不可能達到光速,只有質量為零(在宇宙大爆發時,即大爆炸初始普朗克時期開端之間有很多能量不為0的粒子的質量為0)的
粒子 才可以以光速運動,如因科學研究虛構的“
光子 ”、“
引力子 ”這個名稱。
愛因斯坦 真空 中的光速是一個
物理常數 (符號是c),等於299,792,458m/s。註:光速的方向不恆定。如果在光運行時施加力,那么光的方向進而速度矢量會產生一定的改變。
丹麥 天文學家羅默(OleRomer)在17世紀首次成功地計算出光速。他使用木星的一顆衛星有規律的軌道運動作為計時器,每次這顆衛星被巨大的行星(木星)所掩食,他便記錄下一個“滴答”。但他發現,從地球上觀察,這些滴答的出現並不像預想的那么規律,在一年之中會時而快幾分鐘,時而慢幾分鐘。
羅默計算出,這些時延是木星和地球在繞太陽運動時它們之間的距離變化所引起的。通過計算一年裡地球、木星及其衛星在軌道上的相對位置,他算出了光穿過宇宙空間的速度。
羅默 於1676年向法國科學院提交了他的結果,數值與目前被接受的值之差不超過30%。
對光之本性的理論探討也使人們對光速有所了解。19世紀60年代中期,蘇格蘭科學家詹姆斯·克拉克·麥克斯韋創建了一組方程,描述電磁場在空間中的行為。這個方程的一個解表明,電磁波在
真空 中必須以約為每秒30萬公里的速度傳播,與羅默及其後人的測量結果相當接近。
倫敦皇家研究院的麥可·法拉第用電場和磁場的概念解釋靜電力和磁場力,並表明光會受到磁場影響。這證實了
可見光 事實上是
電磁波譜 中的一部分。對電磁波譜其它部分——微波,紅外線,紫外線,
X射線 和
γ射線 ——傳播速度的直接測量表明,它們在真空中都有相同的速度。用於測量光速的實驗不斷地變得更精確。到20世紀50年代,電子計時裝置已經取代了古老的機械設備。20世紀80年代,通過測量雷射和頻率(f)和波長(λ),運用c=fλ公式計算出了光速(c)。這些計算以米和秒的標準定義為基礎,就像現在一樣,1米定義為氪-86源產生的光的波長的1,650,763.73倍,1秒則定義為銫-133原子超精細躍遷放出的輻射頻率的9,192,631,770倍。這使得c達到非常高的精度,誤差只有十億分之幾。
1983年,光速取代了米被選作定義標準,約定為299,792,458m/s,數值與當時的米定義一致。秒和光速的定義值,表示1米從此定義為光在
真空 中
秒內走過的距離。因此自1983年以來,不管我們對光速的測量作了多少精確的修正,都不會影響到光速值,卻會影響到米的長度。你有多高事實上是由光速定義的。
但光速還定義著比長度更加基本的東西。阿爾伯特·愛因斯坦的工作表明了光速的真正重要性。由於他的功勞,我們知道,光速不僅僅是光子在
真空 中運動的速度,還是連線時間與空間的基本常數。
愛因斯坦年輕的時候曾經問自己,如果人運動的速度快到足以跟上光的腳步,光看起來是什麼樣子的。理論上它看上去像是你身邊一個靜止的峰,但愛因斯坦知道,
麥克斯韋方程組 不允許這種結果出現。他得出結論認為,要么是麥克斯韋的理論不適用於運動中的觀察者,要么是相對運動力學需要更改。
愛因斯坦在他1905年發表的狹義相對論里解決了這個問題。這一理論基於一個通用原則:相對任何以恆定速度運動的觀察者來說,不管這個速度是多少,物理原理及光速都是一樣的。愛因斯坦的狹義相對論使我們對時間和空間的觀念發生了革命性的變化,強調了光速在物理學中的根本地位。
想像你在一枚火箭里,與一道雷射脈衝一同沖入宇宙空間。地球上的觀察者會看到這一脈衝以光速遠去。無論你相對於地球運動的速度為多少,譬如光速的99%罷,光線仍以光速超越你。看起來似乎很荒謬,但這是真的。使這為真的唯一途徑,就是你火箭中的居住者和地球表面的觀察者以不同方式衡量時間和空間。
時間與空間看上去當然是不同的,這依賴於你是在地球上還是在宇宙空間裡。愛因斯坦的廣義相對論將引力描述為
時空 幾何結構的扭曲。這種說法的一個推論,就是始終沿可能的最短路徑穿越時空的光線,在大質量物體附近會彎曲。這在1919年日食期間觀測掠過太陽附近的星光被太陽的質量所彎曲而得到證明。這一觀測使愛因斯坦的理論最終得到接受,並為他贏得了世界性的聲譽。
光速 但按照基本力學原理,如果光線偏轉,它會被加速。這是否將使光速發生變化,動搖相對論的根本原則?在某種意義上是對的:我們從地球上觀察到的光速,在它從太陽附近經過時確實會變化。然而相對論和
光速不變原理 不能被拋棄。
愛因斯坦認識到,引力是無法自由運動的觀察者們經歷的某種幻象。想像從一堵牆上跳下。在
自由落體 的過程中,你不會感動周圍的引力作用,但任何在地面上瞧著你落下來的人,都會解釋說你的運動是引力的作用所致。同樣的說法對空間站中的太空人也適用:他們被提及時總是說成是處在“零重力”環境裡,但從地球的表面往上看,我們會用引力吸引來解釋他們繞地球的軌道運動。所以當我們從地球上觀察時,經過太陽附近的光線看上去彎曲、加速了,但如果我們自由落體地落向太陽,光線看上去會以恆速沿直線經過我們身邊。對任何自由落體的觀察者來說,經過他的光線都以恆定速度運動。不過,它在掠過扭曲其附近時空的大質量物體時,看上去會彎曲和加速。這表明,引力不能被理解為一個場力,而是應該理解為時空的一種內稟特性。
相對論另一個奇怪的推論是,沒有任何物體能加速到光速。不管我們建造動力多么強勁的火箭飛船,它們也永遠不能到達光速。這是因為物體運動得越快,其動能越大,
慣性 也越大。愛因斯坦在他的質能方程中指出,能量和質量或者說慣性相關聯。因此一個物體的動能增加,它的慣性也增加,從而越來越難繼續加速。這是一個收益遞減原理:你對一個物體做的功越多,它就變得越重,加速的效果也越微弱。
把單一電子加速到光速,就需要無限的能量,粒子物理學家們對這一限制深有感觸。
質子 進入美國伊利諾州Batawia費米實驗室的Tevatron加速器時,它們的速度已經達到光速的99%。加速器的最後階段使質子的能量提高了100倍,但速度僅增加到光速的99.99995%,與它們進入加速器的速度相比,提高不足1%。
不過,一直與相對論有衝突的量子理論看上去是允許物質以大於光速的速度運動的。在20世紀20年代,量子論顯示一個系統相隔遙遠的不同組成部分能夠瞬時聯繫。例如,當一個
高能光子 衰變成兩個低能光子時,它們的狀態(例如,是順時針或逆時針自旋)是不定的,直到對它們中間的某一個作出觀察才確定下來。另一個粒子看上去感知到它的同伴被進行了一次觀測,結果是任何對第二個粒子的測量總會得到與對第一個粒子的測量相一致的結果。這樣遠距離的瞬時聯繫,看起來像是一個訊息以無限大的速度在粒子之間傳遞了。它被愛因斯坦稱為“幽靈式的
超距作用 ”,聽起來難以置信,但卻是真實的現象。
1993年,
加利福尼亞大學 伯克利分校的RaymondChiao表明,量子理論還允許另一種超光速旅行存在:量子隧穿。想像朝一堵堅實的牆上踢一個足球,牛頓力學預言它會被彈回,但量子力學預言它還有極小的可能出現在牆的另一面。考慮這種情況的一種途徑,是想像它能“借”到足夠的能量穿越牆壁,並在到達另一面之後立即將能量歸還。這並不違反物理定律,因為最終能量、動量和其它屬性都得到了保存。德國物理學家維納·海森堡的
測不準原理 表明,在一個系統中,總有某些屬性——在這一情況中是能量——的值是不能確定的,只能確定在一個區間內,因此
量子物理學 原理允許系統利用這種不確定性,短時間借到一些額外的能量。在隧穿的情況中,粒子從障礙物的一面消失又從另一面重現的需要幾乎可以忽略不計,障礙物可以任意的厚——不過隨著厚度增加,粒子隧穿的幾率也就迅速地朝零的方向遞減,但請注意,不會等於0(如若這樣,海森堡原理就會被反對,因為0測值為0是確定的)。
Chiao通過測量可見光光子通過特定過濾器的隧穿時間,證明了隧穿“超光速”的隧穿效應存在。為此,他讓這些光子與在相似時間內穿過
真空 的光子進行比較。結果隧穿光子先到達探測器,Chiao證明它們穿越過濾器的速度可能為光速的1.7倍。
1994年,
維也納 技術大學的FerencKraus表明,隧穿時間有一個不依賴於障礙物厚度的上限,這表示光子隧穿障礙物的時間沒有上限。德國
科隆大學 的GunterNimtz也用微波實現了這種“超光速”。他甚至把
莫扎特 第40號交響曲調製在信號上,以4.7倍光速的速度將它傳輸通過12厘米厚的障礙物。
研究歷史 真空中的光速是一個物理
常量 ,國際公認值為c=299792458m/s。17世紀前人們以為光速為無限大,義大利物理學家G.伽利略曾對此提出懷疑,並試圖通過實驗來檢驗他構想,在距離很遠的兩個地方,兩人互相用燈光傳遞信號,最終沒能成功。
艾薩克·牛頓 也接受光速是有限的觀念,在他1704年出版的書《
光學 》中,他提出光每秒鐘可以橫越地球16.6次(相當於210,000公里/秒,比正確值低了30%)。這似乎是他自己的推斷(不能確知他是否有引用或參考羅默的數據)。
1676年,丹麥天文學家奧勞斯·羅默(1644~1710)利用木星衛星的星蝕時間變化證實光是以有限速度傳播的。他利用木星的木衛一在木星在木星圓面上的投影作周期性變化的現象,第一次定量的估計出光速。艾歐的公轉軌道可以用來計算時間,因為它會規律的進入木星的陰影中一段時間。羅默觀測到當地球在最接近木星時,艾歐的公轉周期是42.5小時,當地球遠離木星時,艾歐從陰影中出現的時間會比預測的越來越晚,很明顯的是因為木星與地球的距離增加,使得"信號"要花更多的時間傳遞。光要通過行星之間增加的距離,使得計時的信號在第一次和下一次之間因而延長了額外的時間。當地球向木星接近時,情形則正好相反。羅默觀測到艾歐在接近的40 個軌道周期中周期比遠離的40個軌道周期縮短了22分鐘。以這些觀測為基礎,羅默認為在80個軌道周期中光線要多花費22分鐘行走艾歐與地球之間增加的距離。這意味著地球經歷了80個艾歐軌道周期(42.5小時)的時間,光線只要花22分鐘。這對應於一個地球在軌道上繞著
太陽運動 和光速之間的一個比例。意味著光速是地球的軌道速度的9,300倍,與現 在的數值10,100倍比較,相差較小。但是因為這種觀測是很困難的,因而日後被其他的方法所取代。
在當時,
天文單位 的估計數值是大約1億4千萬公里。
克里斯蒂安·惠更斯 結合了天文單位和羅默的時間估計,每分鐘的光速是地球直徑的1,000倍,他似乎誤解了羅默22分鐘的意思,以為是橫越地球軌道所花費的時間。這相當於每秒220,000公里(136,000英里),比現 在採用的數值低了26%,但仍比當時使用其他已知的物理方法測得的數值為佳。
即使如此,靠著這些觀測,光速是有限的仍不能被大眾滿意的接受(著名的有
吉恩·多米尼克·卡西尼 ),直到在詹姆斯·布雷德里(1728)的觀測之後,光速是無限的想法才被揚棄。布雷德里推論若光速是有限的,則因為地球的軌道速度,會使抵達地球的星光有一個微小角度的偏折,這就是所謂的
光行差 ,他的大小只有1/200度。布雷德里計算的光速為298,000公里/秒(185,000英里/秒),這與現 在的數值只有不到1%的差異。光行差的效應在19世紀已經被充分的研究,最著名的學者是
瓦西里·雅可夫列維奇·斯特魯維 。
1849年,法國物理學家A.H.L.
菲佐 用旋轉齒輪法首次在地面實驗室中成功地進行了光速測量,最早的結果為c=315000千米/秒。1862年,法國
實驗物理學家 J.-B.-L.傅科根據D.F.J.阿拉戈的構想用旋轉鏡法測得光速為c=(298000±500)千米/秒。19世紀中葉J.C.
麥克斯韋 建立了
電磁場理論 ,他根據電磁
波動方程 曾指出,電磁波在
真空 中的傳播速度等於靜電單位電量與電磁單位電量的比值,只要在實驗上分別用這兩種單位測量同一電量(或電流),就可算出電磁波的
波速 。1856年,R.科爾勞施和W.
韋伯 完成了有關測量,麥克斯韋根據他們的數據計算出電磁波在真空中的波速值為3.1074×10^5千米/秒,此值與菲佐的結果十分接近,這對人們確認光是電磁波起過很大作用。
1926年,美國物理學家A.A.
邁克耳孫 改進了傅科的實驗,測得c=(299796±4)千米/秒,他於1929年在真空中重做了此實驗,測得c=299774千米/秒。後來有人用光開關(克爾盒)代替齒輪轉動以改進菲佐的實驗,其精度比旋轉鏡法提高了兩個數量級。1952年,英國實驗物理學家K.D.費羅姆用微波
干涉儀 法測量光速得c=(299792.50±0.10)千米/秒。此值於1957年被推薦為國際推薦值使用,直至1973年。
1972年,美國的K.M.埃文森等人直接測量雷射頻率ν和真空中的波長λ,按公式
(其中v為真空中電磁波的速度,
為真空磁導率,
為真空介電常數)算得c=(299792458±1.2)米/秒。1975年第15屆國際計量大會確認上述光速值作為國際推薦值使用。1983年17屆國際計量大會通過了米的新定義,在這定義中光速c=299792458米/秒為規定值,而
長度單位 米由這個規定值定義。既然真空中的光速已成為定義值,以後就不需對光速進行任何測量了。
1983年,光速取代了保存在巴黎國際計量局的由90%鉑和10%銥的合金製成的米原器被選作定義“米”的標準,並且約定光速嚴格等於299,792,458
m/s ,此數值與當時的米的定義和秒的定義一致。後來,隨著實驗精度的不斷提高,光速的數值有所改變,米被定義為
秒內真空中光通過的路程。
1849年,菲索用
旋轉齒輪法 求得
。他是第一位用實驗方法,測定地面光速的實驗者。 實驗方法大致如下:
光 從半鍍銀面反射後,經高速旋轉的
齒輪 投向
反射鏡 ,再沿原路返回。如果齒輪轉過一齒所需的時間,正好與光往返的時間相等,就可透過半鍍銀面觀測到光,從而根據齒輪的轉速計算出光速。
1862年,法國的
傅科 用
旋轉鏡法 測空氣中的光速,原理和斐索的旋轉齒輪法大同小異,他的結果是
。
第三位在地面上測到光速的是考爾紐。1874年他改進了菲索的旋轉齒輪法,得
。
阿爾伯特·邁克耳孫 改進了傅科的旋轉鏡法,多次測量光速。1879年,得 c = (2.99910±0.00050) ×10^8m/s
;1882年得
。後來,他綜合旋轉鏡法和旋轉齒輪法的特點,發展了
旋轉稜鏡法 ,1924~1927年間,得
。
邁克耳遜在推算真空中的光速時,應該用空氣的群速折射率,可是他用的卻是空氣的相速折射率。這一錯誤在1929年被經改正後,1926年的結果應為
。
60年代雷射器發明,運用穩頻雷射器,可以大大降低光速測量的
不確定度 。
1973年達0.004 ppm,終於在1983年第十七屆
國際計量大會 上作出決定,將真空中的光速定為精確值。
近代測量真空中光速實驗的簡表:
年代
主持人
方式
光速(km/s)
不確定度(km/s)
1907
Rosa、Dorsey
Esu/emu*
299784
15
1928
Karolus 等
克爾盒
299786
15
1947
Essen 等
諧振腔
299792
4
1949
Aslakson
雷達
299792.4
2.4
1951
Bergstand
光電測距儀
299793.1
0.26
1954
Froome
微波干涉儀
299792.75
0.3
1964
Rank 等
帶光譜
299792.8
0.4
1972
Bay 等
穩頻氦氖雷射器
299792.462
0.018
1973
平差
299792.4580
0.0012
1974
Blaney
穩頻CO2雷射器
299792.4590
0.0006
1976
Woods 等
299792.4588
0.0002
1980
Baird 等
穩頻氦氖雷射器
299792.4581
0.0019
1983
國際協定
(規定)
299792.458
(精確值)
(註:esu即electrostatic units的縮寫;emu為electromagnetic units的縮寫。)
研究方法 天文學方法 1676年,丹麥天文學家O.C.羅默利用木星衛星的星蝕時間變化證實光是以有限速度傳播的。1727年,英國天文學家J.布拉得雷利用
恆星光行差 現象估算出光速值為c=303000千米/秒。
羅默的衛星蝕法 光速的測量,首先在天文學上獲得成功,這是因為宇宙廣闊的空間提供了測量光速所需要的足夠大的距離.早在1676年
丹麥 天文學家羅默(1644—1710)首先測量了光速.由於任何周期性的變化過程都可當作時鐘,他成功地找到了離觀察者非常遙遠而相當準確的“時鐘”,羅默在觀察時所用的是木星每隔一定周期所出現的一次衛星蝕.他在觀察時注意到:連續兩次衛星蝕相隔的時間,當地球背離木星運動時,要比地球迎向木星運動時要長一些,他用
光的傳播 速度是有限的來解釋這個現象,光從木星發出(實際上是木星的衛星發出),當地球離開木星運動時,光必須追上地球,因而從地面上觀察木星的兩次衛星蝕相隔的時間,要比實際相隔的時間長一些;當地球迎向木星運動時,這個時間就短一些,因為衛星繞木星的周期不大(約為1.75天),所以上述時間差數,在最合適的時間不致超過15秒(地球的公轉軌道速度約為30千米/秒)。因此,為了取得可靠的結果,當時的觀察曾在整年中連續地進行,羅默通過觀察從衛星蝕的時間變化和
地球軌道 直徑求出了光速,由於當時只知道地球軌道半徑的近似值,故求出的光速只有214300km/s。這個光速值儘管離光速的準確值相差甚遠,但它卻是測定光速歷史上的第一個記錄,後來人們用照相方法測量
木星衛星蝕 的時間,並在地球軌道半徑測量準確度提高后,用羅默法求得的光速為299840±60km/s。
布萊德雷的光行差法 1728年,英國天文學家
布萊德雷 (1693—1762)採用
恆星 的光行差法,再一次得出光速是一有限的物理量,布萊德雷在地球上觀察恆星時,發現恆星的視位置在不斷地變化,在一年之內,所有恆星似乎都在天頂上繞著半長軸相等的橢圓運行了一周,他認為這種現象的產生是由於恆星發出的光傳到地面時需要一定的時間,而在此時間內,地球已因公轉而發生了位置的變化,他由此測得光速為:C=299930千米/秒。
這一數值與實際值比較接近。
以上僅是利用天文學的現象和觀察數值對光速的測定,而在實驗室內限於當時的條件,測定光速尚不能實現。
地面測量方法 光速的測定包含著對光所通過的距離和所需時間的量度,由於光速很大,所以必須測量一個很長的距離和一個很短的時間,大地測量法就是圍繞著如何準確測定距離和時間而設計的各種方法。
最早於1629年艾薩克·畢克曼(Beeckman)提出一項試驗,一人將遵守閃光燈一炮反映過一面鏡子,約一英里。
伽利略 認為光速是有限的,1638年他請二個人提燈籠各爬上相距僅約一公里的山上,第一組人掀開燈籠,並開始計時,對面山上的人看見亮光後掀開燈籠,第一組看見亮光後,停止計時,這是史上著名的測量光速的掩燈方案,這種測量方法實際測到的主要只是實驗者的反應和人手的動作時間。
伽利略測定光速的方法 物理學發展史上,最早提出測量光速的是義大利物理學家伽利略,1607年在他的實驗中,讓相距甚遠的兩個觀察者,各執一盞能遮閉的燈。觀察者A打開燈光,經過一定時間後,光到達觀察者B,B立即打開自己的燈光,過了某一時間後,此信號回到A,於是A可以記下從他自己開燈的一瞬間,到信號從B返回到A的一瞬間所經過的時間間隔t.若兩觀察者的距離為S,則光的速度為
。
因為光速很大,加之觀察者還要有一定的反應時間,所以伽利略的嘗試沒有成功,如果用反射鏡來代替B,那么情況有所改善,這樣就可以避免觀察者所引入的誤差。這種測量原理長遠地保留在後來的一切測定光速的實驗方法之中,甚至在現代測定光速的實驗中仍然採用,但在信號接收上和時間測量上,要採用可靠的方法。使用這些方法甚至能在不太長的距離上測定光速,並達到足夠高的精確度。
旋轉齒輪法 用實驗方法測定光速首先是在1849年由斐索實驗,他用定期遮斷光線的方法(旋轉齒輪法)進行自動記錄。從光源s發出的光經會聚透鏡L1射到半鍍銀的鏡面A,由此反射後在齒輪W的齒a和a’之間的空隙內會聚,再經透鏡L2和L3而達到反射鏡M,然後再反射回來,又通過半鍍鏡A由L4集聚後射入觀察者的眼睛E,如使齒輪轉動,那么在光達到M鏡後再反射回來時所經過的時間△t內,齒輪將轉過一個角度,如果這時a與a’之間的空隙為齒a(或a’)所占據,則反射回來的光將被遮斷,因而觀察者將看不到光,但如齒輪轉到這樣一個角度,使由M鏡反射回來的光從另一齒間空隙通過,那么觀察者會重新看到光,當齒輪轉動得更快,反射光又被另一個齒遮斷時,光又消失。這樣,當齒輪轉速由零而逐漸加快時,在E處將看到閃光,由齒輪轉速v、齒數n與齒輪和M的間距L可推得光速c=4nvL。
在斐索所做的實驗中,當具有720齒的齒輪,一秒鐘內轉動12.67次時,光將首次被擋住而消失,空隙與輪齒交替所需時間為
。
在這一時間內,光所經過的光程為2×8633米,所以光速
。
在對信號的發出和返回接收時刻能作自動記錄的遮斷法除旋轉齒輪法外,在現代還採用克爾盒法,1941年安德孫用克爾盒法測得:c=299776±6km/s,1951年貝格斯格蘭又用克爾盒法測得c=299793.1±0.3km/s。
旋轉鏡法
旋轉鏡法的主要特點是能對信號的傳播時間作精確測量,1851年
傅科 成功地運用此法測定了光速,旋轉鏡法的原理早在1834年1838年就已為
惠更斯 和
阿拉果 提出過,它主要用一個高速均勻轉動的鏡面來代替齒輪裝置,由於光源較強,而且聚焦得較好,因此能極其精密地測量很短的時間間隔。從光源s所發出的光通過半鍍銀的鏡面M1後,經過透鏡L射在繞O軸旋轉的平面反射鏡M2上O軸與圖面垂直,光從M2反射而會聚到凹面反射鏡M3上,M3的曲率中心恰在O軸上,所以光線由M3對稱地反射,並在s′點產生光源的像,當M2的轉速足夠快時,像S′的位置將改變到s〃,相對於可視M2為不轉時的位置移動了△s的距離可以推導出光速值。式中w為M2轉動的角速度,l0為M2到M3的間距,l為
透鏡 L到光源S的間距,△s為s的像移動的距離.因此直接測量w、l、l0、△s,便可求得光速。
在傅科的實驗中:L=4米,L0=20米,△s=0.0007米,W=800×2π弧度/秒,他求得光速值c=298000±500km/s。
另外,傅科還利用這個實驗的基本原理,首次測出了光在介質(水)中的速度v<c,這是對波動說的有力證據。
麥可遜干涉儀 旋轉稜鏡法 美國的
麥可遜 把齒輪法和旋轉鏡法結合起來,創造了旋轉稜鏡法裝置。因為齒輪法之所以不夠準確,是由於不僅當齒的中央將光遮斷時變暗,而且當齒的邊緣遮斷光時也是如此.因此不能精確地測定象消失的瞬時,旋轉鏡法也不夠精確,因為在該法中象的位移△s太小,只有0.7毫米,不易測準。
邁克耳遜 的旋轉鏡法克服了這些缺點,他用一個正八面鋼質稜鏡代替了旋轉鏡法中的旋轉平面鏡,從而光路大大的增長,並利用精確地測定稜鏡的轉動速度代替測齒輪法中的齒輪轉速測出光走完整個路程所需的時間,從而減少了測量誤差。從1879年至1926年,邁克耳遜曾前後從事光速的測量工作近五十年,在這方面付出了極大的勞動,1926年他的最後一個光速測定值為:c=299796km/s,這是當時最精確的測定值,很快成為當時光速的公認值。
實驗室方法 光速測定的天文學方法和大地測量方法,都是採用測定光信號的傳播距離和傳播時間來確定光速的,這就要求要儘可能地增加光程,改進時間測量的準確性。這在實驗室里一般是受時空限制的,而只能在大地野外進行,如斐索的旋輪齒輪法當時是在巴黎的蘇冷與達蒙瑪特勒相距8633米的兩地進行的,傅科的旋轉鏡法當時也是在野外,邁克耳遜當時是在相距35373.21米的兩個山峰上完成的,現代科學技術的發展,使人們可以使用更小更精確地實驗儀器在實驗室中進行光速的測量。
微波諧振腔法 1950年埃森最先採用測定微波波長和頻率的方法來確定光速,在他的實驗中,將微波輸入到圓柱形的
諧振腔 中,當微波波長和諧振腔的幾何尺寸匹配時,諧振腔的圓周長πD和波長之比有如下的關係:πD=2404825λ,因此可以通過諧振腔直徑的測定來確定波長,而直徑則用干涉法測量;頻率用逐級差頻法測定,測量精度達
,在埃森的實驗中,所用微波的波長為10厘米,所得光速的結果為299792.5±1km/s。
雷射測速法 1970年
美國國家標準局 和美國國立物理實驗室最先運用雷射測定光速,這個方法的原理是同時測定雷射的波長和頻率來確定光速(
c=vλ ),由於雷射的頻率和波長的測量精確度已大大提高,所以用雷射測速法的測量精度可達
,比以前已有最精密的實驗方法提高精度約100倍。
除了以上介紹的幾種測量光速的方法外,還有許多十分精確的測定光速的方法。
根據1975年第十五屆國際計量大會的決議,現代真空中光速的準確值是:c=299792.458km/s。
實驗論證 2011年9月,歐洲研究人員發現了一個無法解釋的現象——比光速快60
納秒 的
中微子 。一旦被證實,將顛覆支撐現代物理學的相對論。
而2012年03月03日最新訊息稱,經過數月的反覆檢查,歐洲核子中心日前宣布,衛星定位系統同步接收器可能存在“調校”問題,並高估了中微子運行時間,而把衛星定位系統信號傳送到原子時鐘的光纜可能出現連線“鬆動”並導致低估了粒子包飛行時間。最新一期隸屬美國科學促進會的《科學》雜誌也刊文指出,連線
原子鐘 的光纜出現鬆動,可能導致計算中微子運行時間的原子鐘產生了錯誤結果。
近月來歐洲核子中心已得到證實,該實驗結論是實驗電纜出錯造成的,並沒有顛覆相對論。
歐洲核子中心——大型粒子對撞機
 光速
光速








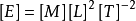








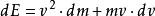


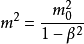



















 愛因斯坦
愛因斯坦
 光速
光速














 麥可遜干涉儀
麥可遜干涉儀

 歐洲核子中心——大型粒子對撞機
歐洲核子中心——大型粒子對撞機




