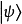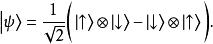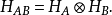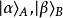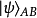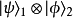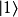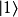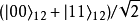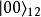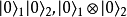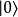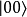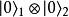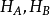在量子力學里，當幾個粒子在彼此相互作用後，由於各個粒子所擁有的特性已綜合成為整體性質，無法單獨描述各個粒子的性質，只能描述整體系統的性質，則稱這現象為量子纏結或量子糾纏（quantum entanglement）。量子糾纏是一種純粹發生於量子系統的現象；在經典力學裡，找不到類似的現象。
基本介紹
歷史,基本概念,數學表述,量子糾纏度量,與不可分性,案例,套用,
歷史
1935年，在普林斯頓高等研究院，愛因斯坦、博士後羅森、研究員波多爾斯基合作完成論文《物理實在的量子力學描述能否被認為是完備的？》，並且將這篇論文發表於5月份的《物理評論》。這是最早探討量子力學理論對於強關聯繫統所做的反直覺預測的一篇論文。在這篇論文裡，他們詳細表述EPR佯謬，試圖借著一個思想實驗來論述量子力學的不完備性質。他們並沒有更進一步研究量子糾纏的特性。
薛丁格閱讀完畢EPR論文之後，有很多心得感想，他用德文寫了一封信給愛因斯坦，在這封信里，他最先使用了術語Verschränkung（他自己將之翻譯為“糾纏”），這是為了要形容在EPR思想實驗裡，兩個暫時耦合的粒子，不再耦合之後彼此之間仍舊維持的關聯。不久之後，薛丁格發表了一篇重要論文，對於“量子糾纏”這術語給予定義，並且研究探索相關概念。薛丁格體會到這概念的重要性，他表明，量子糾纏不只是量子力學的某個很有意思的性質，而是量子力學的特徵性質；量子糾纏在量子力學與經典思路之間做了一個完全切割。如同愛因斯坦一樣，薛丁格對於量子糾纏的概念並不滿意，因為量子糾纏似乎違反在相對論中對於信息傳遞所設定的速度極限。後來，愛因斯坦更譏諷量子糾纏為鬼魅般的超距作用。
EPR論文很顯然地引起了眾多物理學者的興趣，啟發他們探討量子力學的基礎理論。但是除了這方面以外，物理學者認為這論題與現代量子力學並沒有什麼牽扯，在之後很長一段時間，物理學術界並沒有特別重視這論題，也沒有發現EPR論文可能有什麼重大瑕疵。EPR論文試圖建立定域性隱變數理論來替代量子力學理論。1964年，約翰·貝爾提出論文表明，對於EPR思想實驗，量子力學的預測明顯地不同於定域性隱變數理論。概略而言，假若測量兩個粒子分別沿著不同軸向的自旋，則量子力學得到的統計關聯性結果比定域性隱變數理論要強很多，貝爾不等式定性地給出這差別，做實驗應該可以偵測出這差別。因此，物理學者做了很多檢試貝爾不等式的實驗。
1972年，約翰·克勞澤與史達特·弗利曼（Stuart Freedman）首先完成這種檢試實驗。1982年，阿蘭·阿斯佩的博士論文是以這種檢試實驗為題目。他們得到的實驗結果符合量子力學的預測，不符合定域性隱變數理論的預測，因此證實定域性隱變數理論不成立。但是，每一個相關實驗都存在有漏洞，這造成了實驗的正確性遭到質疑，在作總結之前，還需要完成更多精確的實驗。
基本概念
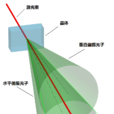
假設一個零自旋中性π介子衰變成一個電子與一個正電子。這兩個衰變產物各自朝著相反方向移動。電子移動到區域A，在那裡的觀察者“愛麗絲”會觀測電子沿著某特定軸向的自旋；正電子移動到區域B，在那裡的觀察者“鮑勃”也會觀測正電子沿著同樣軸向的自旋。在測量之前，這兩個糾纏粒子共同形成了零自旋的“糾纏態”
，是兩個直積態（product state）的疊加，以狄拉克標記表示為
在圓括弧內的第一項表明，電子的自旋為上旋若且唯若正電子的自旋為下旋；第二項表明，電子的自旋為下旋若且唯若正電子的自旋為上旋。兩種狀況疊加在一起，每一種狀況都有可能發生，不能確定到底哪種狀況會發生，因此，電子與正電子糾纏在一起，形成糾纏態。假若不做測量，則無法知道這兩個粒子中任何一個粒子的自旋，根據哥本哈根詮釋，這性質並不存在。這單態的兩個粒子相互反關聯，對於兩個粒子的自旋分別做測量，假若電子的自旋為上旋，則正電子的自旋為下旋，反之亦然；假若電子的自旋下旋，則正電子自旋為上旋，反之亦然。量子力學不能預測到底是哪一組數值，但是量子力學可以預言，獲得任何一組數值的機率為50%。
粒子沿著不同軸向的自旋彼此之間是不相容可觀察量，對於這些不相容可觀察量作測量必定不能同時得到明確結果，這是量子力學的一個基礎理論。在經典力學裡，這基礎理論毫無意義，理論而言，任何粒子性質都可以被測量至任意準確度。貝爾定理意味著一個事實，一個已被實驗檢試的事實，即對兩個不相容可觀察量做測量得到的結果不遵守貝爾不等式。因此，基礎而言，量子糾纏是個非經典現象。
不確定性原理的維持必須倚賴量子糾纏機制。例如，構想先前的一個零自旋中性π介子衰變案例，兩個衰變產物各自朝著相反方向移動，分別測量電子的位置與正電子的動量，假若量子糾纏機制不存在，則可借著守恆定律預測兩個粒子各自的位置與動量，這違反了不確定性原理。由於量子糾纏機制，粒子的位置與動量遵守不確定性原理。
從以相對論性速度移動的兩個參考系分別測量兩個糾纏粒子的物理性質，儘管在每一個參考系，測量兩個粒子的時間順序不同，獲得的實驗數據仍舊違反貝爾不等式，仍舊能夠可靠地複製出兩個糾纏粒子的量子關聯。
數學表述
設定子系統A、B的量子態分別為
，假若複合系統的量子態
不能寫為張量積
，則稱這複合系統為子系統A、B的糾纏系統，兩個子系統A、B相互糾纏。
量子糾纏度量
量子糾纏與量子系統失序現象、量子信息喪失程度密切相關。量子糾纏越大，則子系統越失序，量子信息喪失越多；反之，量子糾纏越小，子系統越有序，量子信息喪失越少。因此，馮諾伊曼熵可以用來定量地描述量子糾纏，另外，還有其它種度量也可以定量地描述量子糾纏。對於兩體複合系統，這些糾纏度量較常遵守的幾個規則為：
- 糾纏度量必須映射從密度算符至正實數。
- 假若整個複合系統不處於糾纏態，則糾纏度量必須為零。
- 對於純態複合系統，糾纏度量必需約化為馮諾伊曼熵。
- 對於命定性的定域運算與經典通訊（local operation and classical communication）變換，糾纏度量不會增加。
對於兩體純態，只有馮諾伊曼熵能夠量度量子糾纏，因為只有它能夠滿足某些量度量子糾纏必須遵守的判據。對於混合態，使用馮諾伊曼熵並不是能夠量度量子糾纏的獨有方法。
與不可分性
假設一個量子系統是由幾個處於量子糾纏的子系統組成，而整體系統所具有的某種物理性質，子系統不能私自具有，這時，不能夠對子系統給定這種物理性質，只能對整體系統給定這種物理性質，它具有“不可分性”。不可分性不一定與空間有關，處於同一區域的幾個物理系統，只要彼此之間沒有任何糾纏，則它們各自可擁有自己的物理性質。物理學者艾雪·佩雷斯（Asher Peres）給出不可分性的數學定義式，可以計算出整體系統到底具有可分性還是不可分性。假設整體系統具有不可分性，並且這不可分性與空間無關，則可將它的幾個子系統分離至兩個相隔遙遠的區域，這動作凸顯出不可分性與定域性的不同──雖然幾個子系統分別處於兩個相隔遙遠的區域，仍舊不可將它們個別處理。在EPR佯謬里，由於兩個粒子分別處於兩個相隔遙遠的區域，整體系統被認為具有可分性，但因量子糾纏，整體系統實際具有不可分性，整體系統所具有明確的自旋z分量，兩個粒子各自都不具有。
案例
以兩顆向相反方向移動但速率相同的電子為例，即使一顆行至太陽邊，一顆行至冥王星邊，在如此遙遠的距離下，它們仍保有關聯性（correlation）；亦即當其中一顆被操作（例如量子測量）而狀態發生變化，另一顆也會即時發生相應的狀態變化。如此現象導致了鬼魅似的超距作用之猜疑，仿佛兩顆電子擁有超光速的秘密通信一般，似與狹義相對論中所謂的定域性原理相違背。這也是當初阿爾伯特·愛因斯坦與同僚玻理斯·波多斯基、納森·羅森於1935年提出的EPR佯謬來質疑量子力學完備性的理由。
具有量子糾纏的兩顆電子——電子1和電子2，其自旋性質之糾纏態可以下面式子為例：
太陽邊的科學家決定對電子1做投影式量子測量，其測到的隨機性結果不是就是。當其測量結果顯示為狀態，則冥王星的科學家在此之後，或很近、或較遠的時間點對電子2做測量，必定會測到狀態。因為投影式量子測量已經將原先量子態
選擇性地坍縮到
，也可寫成
。這樣，可以從電子1狀態是
知道選擇到
這一邊。
注意到：
已經是兩個成員系統各自量子態的張量積，所以測量後狀態已非糾纏態。
套用
量子糾纏是一種物理資源，如同時間、能量、動量等等，能夠萃取與轉換。套用量子糾纏的機制於量子信息學，很多平常不可行的事務都可以達成：
- 量子密鑰分發能夠使通信雙方共同擁有一個隨機、安全的密鑰，來加密和解密信息，從而保證通信安全。在量子密鑰分發機制里，給定兩個處於量子糾纏的粒子，假設通信雙方各自接受到其中一個粒子，由於測量其中任意一個粒子會摧毀這對粒子的量子糾纏，任何竊聽動作都會被通信雙方偵測發覺。
- 量子隱形傳態套用先前傳送點與接收點分享的兩個量子糾纏子系統與一些經典通訊技術來傳送量子態或量子信息（編碼為量子態）從傳送點至相隔遙遠距離的接收點。
- 量子算法（quantum algorithm）的速度時常會勝過對應的經典算法很多。但是，在量子算法裡，量子糾纏所扮演的角色，物理學者尚未達成共識。有些物理學者認為，量子糾纏對於量子算法的快速運算貢獻很大，但是，只倚賴量子糾纏並無法達成快速運算。
- 在量子計算機體系結構里，量子糾纏扮演了很重要的角色。例如，在一次性量子計算機（one-way quantum computer）的方法裡，必須先製備出一個多體糾纏態，通常是圖形態（graph state）或簇態（cluster state），然後借著一系列的測量來計算出結果。
