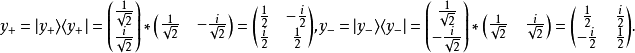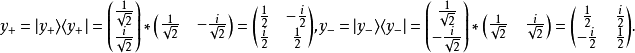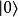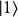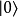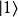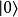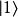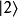基本介紹
- 中文名:量子位元
- 外文名:Qubit
- 領域:量子力學
定義,按方向所采的諸多表示法,z方向,x方向,y方向,量子三元,
定義
具有量子特性的系統(通常為雙態系統,如自旋1/2粒子),選定兩個相互正交的本徵態,分別以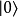 (采狄拉克標記右括向量表示)和
(采狄拉克標記右括向量表示)和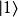 代表。當對此系統做投影式量子測量時,會得到的結果必為這兩個本徵態之一,以特定機率比例出現。此外,這兩個本徵態可以複數係數做線性疊加得到諸多新的量子態
代表。當對此系統做投影式量子測量時,會得到的結果必為這兩個本徵態之一,以特定機率比例出現。此外,這兩個本徵態可以複數係數做線性疊加得到諸多新的量子態
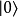
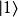
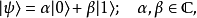
而從量子力學得知,這些線性疊加態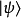 的兩個複數係數,必須要求各自絕對值平方相加之和為1,也就是:
的兩個複數係數,必須要求各自絕對值平方相加之和為1,也就是:
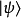
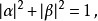
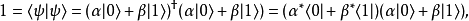
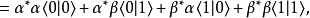
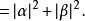
和(古典)位元“非0即1”有所不同,量子位元可以“又0又1”的狀態存在,所謂“又0又1”即上述無限多種
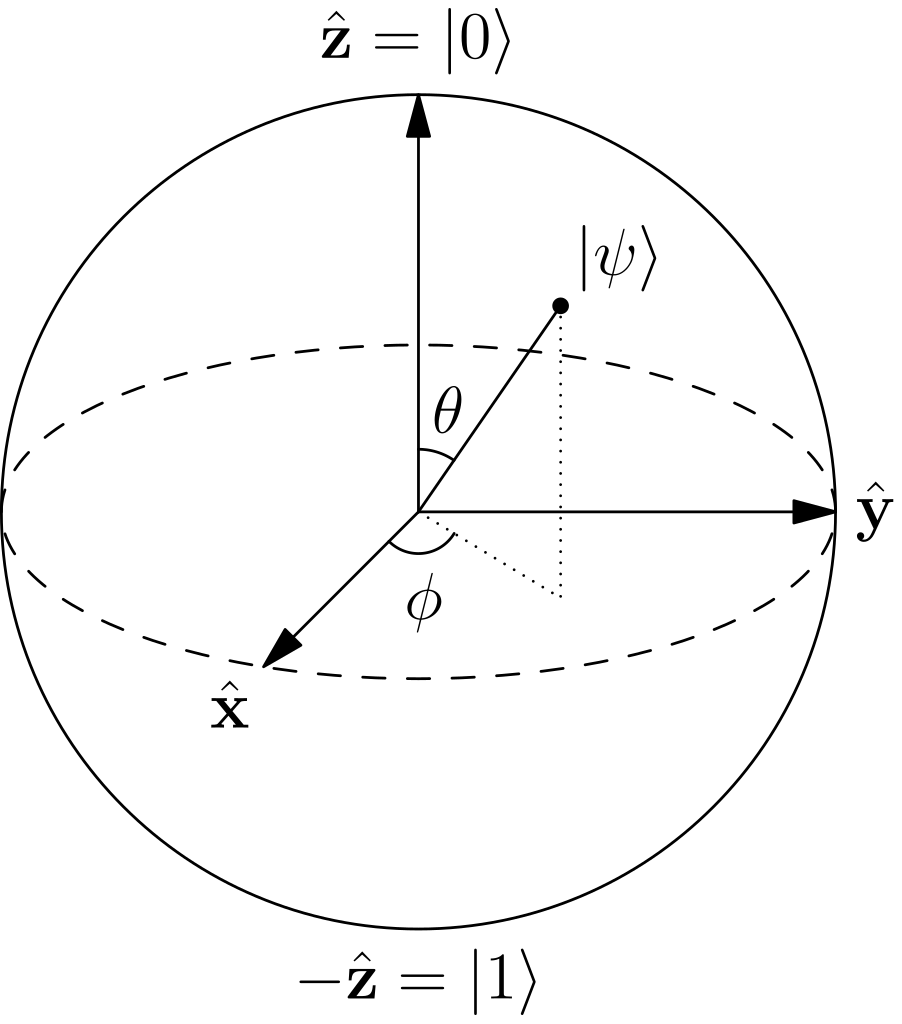
量子位元通常會採用一種幾何表示法將之圖像化,此表示法稱之為布洛赫球面。
按方向所采的諸多表示法
z方向
向量: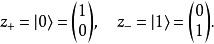
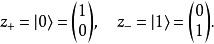
密度矩陣: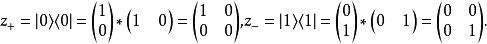
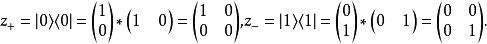
x方向
向量: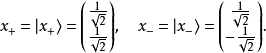
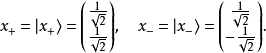
密度矩陣: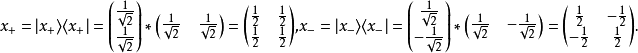
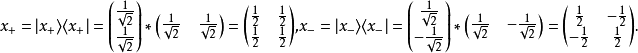
y方向
向量: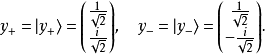
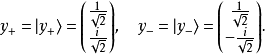
密度矩陣: