基本介紹
- 中文名:四維矢量
- 外文名:Four-dimension vector
- 數學性質:兩個事件之間的矢量差
- 動力學:物體運動的速度隨著時間改變
- 套用學科:數學
- 所屬領域:數學和物理學
數學性質
透過洛倫茲變換,給予一個事件對於某慣性參考系的四維坐標,即可計算出這事件對於另外一個慣性參考系的四維坐標。這是個很優良的物理性質。當研究物理現象時,所涉及的四維矢量,最好都能夠具有這優良的性質。這樣,可以使得數學分析更加精緻犀利。


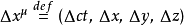



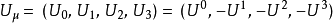





動力學





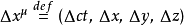



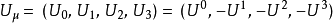







四維矢量,是在狹義相對論里,四維矢量 (four-vector) 是實值四維矢量空間裡的矢量。這四維矢量空間稱為閔可夫斯基時空。四維矢量的分量分別為時間與三維位置。在閔...
四維空間不同於三維空間,四維空間指的是標準歐幾里得空間,可以拓展到n維;四維時空指的是閔可夫斯基空間概念的一種誤解。人類作為三維物體可以理解四維時空(三個空間...
四維彩超即四維(four-dimensional,4D)醫學彩色超聲成像技術,也可用於指代採用這種技術的檢查或實現這種技術的儀器。四維彩超是在三維(three-dimensional,3D)醫學彩色...
第一、電磁四維勢乃是一個四維矢量。使用標準四維矢量變換規則,假若知道在某慣性參考系的電磁四維勢,很容易就可以計算出在其它慣性參考系的數值。 第二、經典電磁...
《矢量新說》,桂祖華著。本書是對矢量進行深入研究與探討的學術著作。該書共分五章,引進了矢量倍積、輪換矢量、廣矢量和二重矢量等新概念,指出了它們在幾何方面...
波矢是波的矢量表示方法。...... 波矢在狹義相對論背景下可定義為四維矢量。波矢有兩種常見的定義,區別在於振幅因子是否乘以 ,兩種定義分別用於物理學和晶體學以及...
“4D”是“四維”的縮寫。第四維是指時間這個矢量。對於超聲學來說,4D超聲技術是新近發展的技術,也是GE公司的獨家技術。...
利用w=ict 將事件坐標(t,x,y,z) 改寫為四維矢量 (w,x,y,z),則其模方是洛倫茲不變數(時空距離的相反數),此時洛侖茲變換成為該矢量的旋轉變換。用方程組...
而洛倫茲規範下矢量勢和標量勢的方程(11)其協變形式即為:(12)式中, 在洛倫茲變換下,三維力密度(f1,f2,f3)和功率密度w亦配成四維矢量(f0,f1,f2,f3),...
在經典物理中不同類別的物理量,透過相對性原理在狹義與廣義相對論中自然的統合:比如時間與空間結合為四維位置,能量與動量結合為四維動量。這些四維矢量與所使用的...
