基本介紹
平移變換

三種伽利略變換
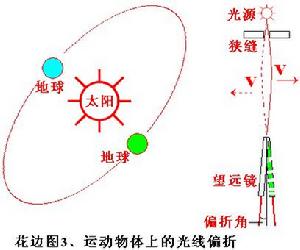 運動物體上的光線也發生了彎曲
運動物體上的光線也發生了彎曲

 運動物體上的光線也發生了彎曲
運動物體上的光線也發生了彎曲伽利略變換是經典力學中用以在兩個只以均速相對移動的參考系之間變換的方法,屬於一種被動態變換。伽利略變換明顯成立的公式在物體以接近光速運動時、亦或者是電磁...
洛倫茲變換(Lorentz transformation)是狹義相對論中兩個作相對勻速運動的慣性參考系(S和S′)之間的坐標變換,是觀測者在不同慣性參考系之間對物理量進行測量時所...
後伽利略變換是天文學專有名詞。來自中國天文學名詞審定委員會審定發布的天文學專有名詞中文譯名,詞條譯名和中英文解釋數據著作權由天文學名詞委所有。...
慣性系坐標變換(coordinate transformation of inertial frame)是指慣性系中的坐標變換。...
洛倫茲變換是觀測者在不同慣性參照系之間對物理量進行測量時所進行的轉換關係,在數學上表現為一套方程組。洛倫茲變換因其創立者——荷蘭物理學家亨德里克·洛倫茲...
洛侖茲變換是描述狹義相對論空間中各參考系間關係的變換。它最早由洛侖茲從以太說推出,用以解決經典力學與經典電磁學間的矛盾(即麥可孫-莫雷實驗的零結果)。後...
《牛頓力學的新時空變換:Z變換(廣義的伽利略變換)》以獨特的視角和思路,通過嚴謹的演繹與論證,首次發現唯一存在的適應於“兩坐標系有相對運動且真空中光速為有限值...
而牛頓時空理論(或伽利略變換)中的時間沒有辦法在現實世界中實現。為使用光信號對鐘,愛因斯坦假定了單向光速是個常數且與光源的運動無關(光速不變原理)。此外,他...
力學相對性原理(伽利略相對性原理)僅指經典力學定律在任何慣性參考系(慣性系)中數學形式不變,換言之,所有慣性系都是等價(平權)的。伽利略用物理學原理為哥白尼地...
第2章愛因斯坦的洛倫茲變換誕生之初的失誤11第3章洛倫茲變換與伽利略變換153.1洛倫茲變換153.2伽利略變換163.3質疑愛因斯坦的非同時性時間變換式18...
則相對速度為u2-u1。相對速度不隨慣性參考系的選取而改變,即在伽利略變換中,相對速度是一個不變的矢量,所以相對速度也有方向,方向為絕對值大的方向。...
在愛因斯坦以前,人們廣泛的關注於麥克斯韋方程組在伽利略變換下不協變的問題,也有人(如龐加萊和洛倫茲)注意到愛因斯坦提出狹義相對論所基於的實驗(如麥可孫-莫雷...
19世紀末由於牛頓力學和(蘇格蘭數學家)麥克斯韋(1831~1879年)電磁理論趨於完善,一些物理學家認為“物理學的發展實際上已經結束”,但當人們運用伽利略變換解釋光的傳播...
相對慣性系作等速直線運動的任何參考系都是慣性系,因為在這些參考系中牛頓運動定律都成立(見伽利略變換),即在相對慣性系作等速直線運動的任何參考系中,力學規律的...
