第一個張量對它的前兩個指標是對稱的,而第二個張量對前三個指標是對稱的。若有這樣的張量,它的兩個反變指標或共變指標互換時,張量的分量值改變符號而大小不變,則該張量稱為反對稱或斜對稱的。
基本介紹
- 中文名:反對稱張量
- 外文名:antisymmetric tensor
- 定義:張量的分量值改變符號而大小不變
- 套用學科:量子力學術語
- 範疇:數理科學
- 涉及:張量
概念
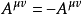
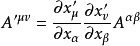
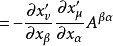
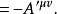
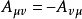
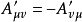
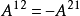
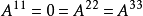
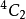
基本原理
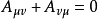
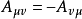
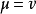
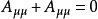
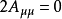
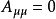
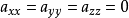
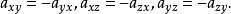
 圖1
圖1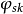
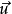
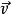

第一個張量對它的前兩個指標是對稱的,而第二個張量對前三個指標是對稱的。若有這樣的張量,它的兩個反變指標或共變指標互換時,張量的分量值改變符號而大小不變,則該張量稱為反對稱或斜對稱的。
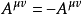
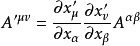
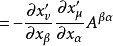
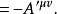
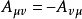
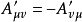
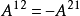
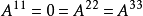
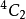
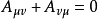
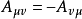
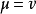
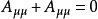
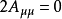
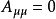
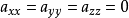
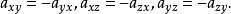
 圖1
圖1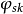
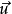
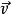
第一個張量對它的前兩個指標是對稱的,而第二個張量對前三個指標是對稱的。若有這樣的張量,它的兩個反變指標或共變指標互換時,張量的分量值改變符號而大小不...
對稱張量是各分量關於指標對稱的張量,表示r階反變張量全體。x是對稱張量的充分必要條件是它的分量關於各指標是對稱的,x是反對稱張量的充分必要條件是它的分量關於...
兩個張量之間並積和縮並的聯合運算。例如,在極分解定理中,三個二階張量R、U和V中一次點積R·U和V·R的結果是二階張量F。5. 對稱化和反稱化...
對稱化運算元(symmetrization operator)是作用於反對稱張量上的運算元。張量是向量概念的綜合,可用以代表各向量間的關係。例如彈性張量把彈性體上每一點的變形與外加應力...
反對稱化運算元(anti-symmetrization operator)是作用於反對稱張量上的運算元。...... 反對稱化運算元(anti-symmetrization operator)是作用於反對稱張量上的運算元。...
1.7.3標量與張量相乘281.7.4張量與張量並乘281.7.5張量的縮並281.7.6張量的點積291.7.7轉置張量301.7.8張量的對稱化與反對稱化31...
在評估過所有分量後,可以得到一個二階、反對稱、協變張量 :場強張量在量子電動力學與量子場論中的角色 編輯 在量子電動力學中的拉格朗日量是從相對論建立的經典...
。特別地(見下),測地線方程確定聯絡的對稱部分,而撓率張量確定反對稱部分。扭率張量撓率形式 撓率形式,是撓率的另一種刻畫,適用於M的標架叢FM。這個主叢裝備有...
完全對稱化子(completely symmetrizer)是張量空間上的一種投影運算元,有時也稱為對稱化子。多重線性代數的重要概念。定義有張映射的一種向量空間。具體定義有多種不...
1.8.3反對稱二階張量 1.9二階張量的不變數、主值和主方向,正則與退化二階張量 1.9.1二階張量的不變數 1.9.2對稱:階張量的主值和主方向 1.9.3非對稱...
§1.9 幾個重要的特殊張量 §1.10 笛卡兒張量 §1.11 矢量乘積的張量表示 第二章 張量代數 §2.1 張量的加法(減法) §2.2 對稱張量、反對稱張量 §2.3 ...
9.4Mathematica的張量運算 習題 附錄A示範例題 張量概念 逆變矢量、協變矢量和張量 克羅內克符號δ 張量的基本運算 對稱張量和反對稱張量 矩陣 線元和度...
在微分幾何中,類似度量張量,里奇張量也是一個在黎曼流形每點的切空間上的對稱雙線性形式。以格雷戈里奧·里奇-庫爾巴斯托羅(Gregorio Ricci-Curbastro)為名的里奇...
也就是說曲率張量衡量協變導數的反交換性。線性變換也稱曲率變換。黎曼曲率張量對稱性和恆等式 編輯 黎曼曲率張量有如下的對稱性:最後一個恆等式由里奇(Ricci)發現...
列維-奇維塔符號(Levi-Civita symbol),特別線上性代數,張量分析和微分幾何等數學...其它名稱包括排列符號,反對稱符號或交替符號,是有關於反對稱的屬性與排列的定義...
格拉斯曼空間亦稱反對稱張量空間。是一個最常見的張量對稱類,即當G=Sm,χ=ε(符號特徵標)時的張量對稱類。通常寫為:[1] 可合元素則寫為:...
相對論角動量的關係式則不那么明顯…經典力學中的角動量定義為位置x與動量p的叉積,產生了一個贗矢量x×p;其亦可透過外積產生一個二階反對稱張量x∧p。...
外微分形式,又稱微分形式,是微分流形上定義的反對稱協變張量場。...... 外微分形式,又稱微分形式,是微分流形上定義的反對稱協變張量場。中文名 外微分形式 ...
