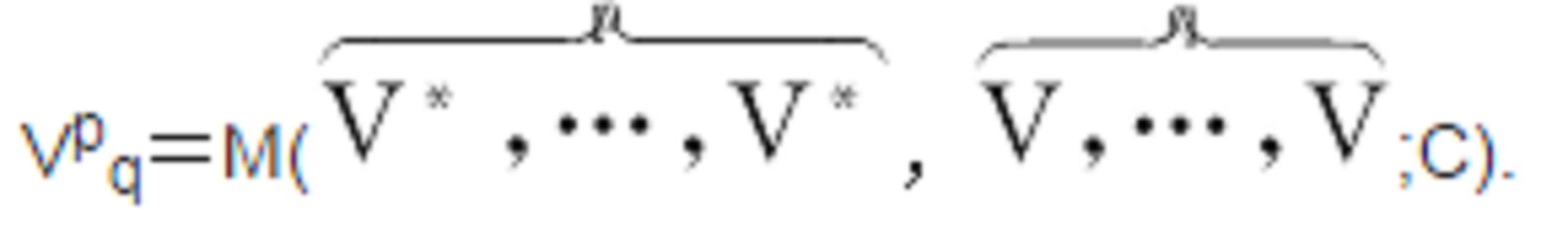對稱化運算元(symmetrization operator)是作用於反對稱張量上的運算元。張量是向量概念的綜合，可用以代表各向量間的關係。例如彈性張量把彈性體上每一點的變形與外加應力聯繫起來。張量計算最初的發展是與微分幾何相聯繫的，也是愛因斯坦在系統地闡述廣義相對論時所用的基本工具。
基本介紹
- 中文名：對稱化運算元
- 外文名：symmetrization operator
- 領域：數學
- 學科：多重線性代數
- 定義：作用於反對稱張量上的運算元
- 對象：反對稱張量
概念,張量,張量空間,多重線性代數,混合張量,
概念
對稱化運算元作用於反對稱張量上的運算元。對任意的x∈Tr(V)，令：
張量
張量是向量概念的綜合，可用以代表各向量間的關係。例如彈性張量把彈性體上每一點的變形與外加應力聯繫起來。張量計算最初的發展是與微分幾何相聯繫的，也是愛因斯坦在系統地闡述廣義相對論時所用的基本工具。
n維空間中的一個量，它具有nr個分量，用
表示，它的每個分量都是坐標的函式；在坐標變換下，這些分量按照一定的規律作線性變換。r稱為張量的階。
張量是矢量及矩陣概念的推廣。標量是零階張量;向量是一階張量；矩陣是二階張量。三階張量(它的分量用Tijr表示)就像是一個“立體矩陣”。
在1900年，張量首先在彈性理論中使用。“張量”原來的含義是“張緊”與“張開”。
1892年起，里奇(C.G.Ricci，意，1853—1925)與列維·奇維塔(T.Levi-Civita，意，1873—1941)開始建立張量分析的理論，成為黎曼幾何與廣義相對論的一種工具。
為了簡便，在張量列式或計算時，常按求和約定將求和號略去。
張量空間
張量空間(tensor space)是多重線性代數的重要概念，定義是有張映射的一種向量空間。多重線性代數式代數學的一個重要分支。可以將它看做是線性代數的發展。它是伴隨著微分幾何、現代分析、群表示論、理論物理、量子力學等學科發展起來的，並且在這些學科中已得到重要的套用。具體定義有多種不同的形式。例如，可定義為：設P是一個向量空間，若存在張映射
：V1×V2×…×Vm→P使得〈Im
〉=P，則稱P為V1，V2，…，Vm的帶有張映射的張量空間；或稱P為V1，V2，…，Vm的張量積空間；或簡稱P為V1，V2，…，Vm的張量積，記為：
多重線性代數
代數學的一個重要分支。可以將它看做是線性代數的發展。它是伴隨著微分幾何、現代分析、群表示論、理論物理、量子力學等學科發展起來的，並且在這些學科中已得到重要的套用。
多重線性代數形成為一個學科還是近幾十年來的事，值得提出的是20世紀50年代，布爾巴基(Bourbaki，N.)論述多重線性代數的書及20世紀60年代，葛瑞布(Greub，W.)的多重線性代數專著(第一版)，特別是從1973年，由馬庫斯(Marcus，M.)和湯普森(Thompson，R.C.)創辦了國際性的《線性和多重線性代數》(Linear and Multilinear Algebra)雜誌以及同年馬庫斯出版了經典性著作《有限維多重線性代數》以來，多重線性代數的發展進入了一個活躍的新階段，這當中以梅里斯(Merris，R.)等人研究高階特徵標的張量對稱類所獲得的成果最為突出。
多重線性代數研究的內容包括：多重線性映射、具有一定對稱性質的多重線性映射、張量空間、張量對稱類、張量代數、對稱張量代數、格拉斯曼代數、外代數、克利福德代數及其表示理論等。這裡的前半部分只就常用的有限維多重線性代數來敘述，對於以泛性質手段處理的無限維情形可參看葛瑞布(Greub，W.H.)於1978年著的《多重線性代數》(第二版)。對可換環上建立在環模上的多重線性代數則可參看諾茨考特(Northcott，D.G.)於1984年著的《多重線性代數》。
多重線性代數這部分詞條的向量空間一般是指一個特徵為零的域K上的(向量)空間，但當關係到內積和群的任意特徵標時，為了敘述簡明則只在複數域C上討論.域上的多重線性代數的主要概念與結果都可用模論的工具推廣到交換環上的多重線性代數，這裡不再一一提及。交換環上的多重線性代數在模論、同調代數、代數K理論、代數幾何等學科中都有重要套用。
混合張量
混合張量(mixed tensor)是一類張量。向量空間及其對偶空間張量積的元素。張量是向量概念的綜合，可用以代表各向量間的關係。例如彈性張量把彈性體上每一點的變形與外加應力聯繫起來。張量計算最初的發展是與微分幾何相聯繫的，也是愛因斯坦在系統地闡述廣義相對論時所用的基本工具。
張量空間：
(記為Vq)中的元素稱為p重反變q重共變張量；或稱為(p，q)重混合張量，其中V是C上向量空間，V*=L(V，C)是V的對偶空間。混合張量也指：
中的多重線性函式。可以定義張映射使：
