完全對稱化子(completely symmetrizer)是張量空間上的一種投影運算元,有時也稱為對稱化子。多重線性代數的重要概念。定義有張映射的一種向量空間。具體定義有多種不同的形式。張量空間對於多重線性代數的重要性如同向量空間對於線性代數的重要性。
基本介紹
- 中文名:完全對稱化子
- 外文名:completely symmetrizer
- 領域:數學
- 空間:張量空間
- 別稱:對稱化子
- 性質:投影運算元
概念
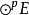
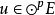

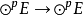
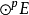
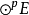
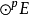
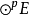
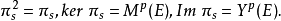
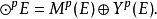
向量空間
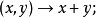
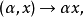

張量空間
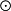


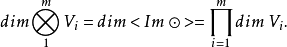
投影運算元
張量
對稱張量

完全對稱化子(completely symmetrizer)是張量空間上的一種投影運算元,有時也稱為對稱化子。多重線性代數的重要概念。定義有張映射的一種向量空間。具體定義有多種不同的形式。張量空間對於多重線性代數的重要性如同向量空間對於線性代數的重要性。
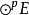
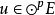

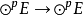
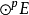
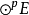
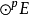
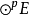
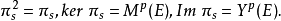
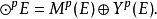
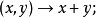
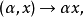

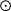


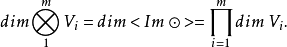

完全對稱化子(completely symmetrizer)是張量空間上的一種投影運算元,有時也稱為對稱化子。多重線性代數的重要概念。定義有張映射的一種向量空間。具體定義有多種不...
或(0,p)型張量空間 的線性變換 稱為對稱化子,這裡 表示p次對稱群。任意張量α在 下的像是對稱張量。的對稱張量構成的子空間是關於張量表示 的不變子空間。參...
按照博克里斯和馬修斯的觀點,對稱因子是一個控制電能向化學能轉換的係數。與此相似的是多戈納澤提出的概念,他認為對稱因子是金屬中一個軌道被占據的幾率的度量。...
在自然界千變萬化的運動演化過程中,運動的多樣性顯現出了各式各樣的對稱性。在...這叫做規範對稱性。 完全等效的規範對稱性可套用到電磁相互作用,諸如在電磁場中...
左右對稱在建築藝術中有大量套用,但是人們也注意到完全的左右對稱也許顯得太死板,...遵循現代人文教育和公民教育的理念,秉承通達民情,化育人心的中國傳統教育精神,...
對稱操作是指能使一個對稱圖像復原的每一種動作。 (對稱性的圖像是能經過一種以上不改變其中任何兩點間距離的動作後復原的圖像)symmetry operation又稱對稱動作。...
3-3.子群、陪集和互換群的定義 練習和套用 §4.操作的變換和有關原理 4-1...2-6.方陣的相似換算、特徵值和對角化 練習和套用 第二章 對稱換算和方陣表象...
倒轉180度後,與原圖形完全一樣,仍然可以清晰地讀出四個單詞的字樣!對稱字中文字型 編輯 由於漢字結構複雜,所以對稱字的製作也較為複雜。但一旦形成,便會具有別樣...
若在饋電點將天線分為兩半,而這兩半的幾何結構形式和尺寸完全相同,則稱為對稱...會導致天線的副瓣電平升高,增益降低,為了降低寄生阻抗的影響,天線極子連線處用切...
二者相輔相成,兩圖形成中心對稱,必有對稱中點,而點只有能使兩個圖形旋轉180°後完全重合才稱為對稱中點。識別一個圖形是否是中心對稱圖形就是看是否存在一點,使...
對稱面舉例說明 現在考慮幾個說明分子對稱面的例子。一種極端情況是完全沒有對稱面的分子。這種分子的一種普通類型是非平面的分子,分子中每種原子的數目都是奇數。...
那么它搜尋完全部密鑰就需要將近2285年的時間,因此DES算法是一種很可靠的加密...對稱密鑰:RC算法RC4算法的原理是“攪亂”,它包括初始化算法和偽隨機子密碼生成...
左右對稱在建築藝術中有大量套用,但是人們也注意到完全的左右對稱也許顯得太死板,...“科普中國”是為我國科普信息化建設塑造的全... 什麼是權威編輯 查看編輯版本...
在魔方最少步驟還原中,若某狀態可由某一還原態經一系列操作X1X2...Xn達到,則稱以下兩類狀態為當前狀態的對稱態: 取任意一還原態,執行X1X2...Xn並在之前...
