半有界運算元(semi-bounded operator)是上半有界運算元和下半有界運算元的統稱。
基本介紹
- 中文名:半有界運算元
- 外文名:semi-bounded operator
- 適用範圍:數理科學
簡介
推論
線性運算元
正定運算元
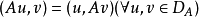


半有界運算元(semi-bounded operator)是上半有界運算元和下半有界運算元的統稱。
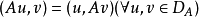


半有界運算元(semi-bounded operator)是上半有界運算元和下半有界運算元的統稱。...... 半有界運算元(semi-bounded operator)是上半有界運算元和下半有界運算元的統稱。...
泛函分析中一種重要的運算元。運算元(映射)有線性和非線性之分.線性運算元又分為有界和無界兩類,有界線性運算元是線性賦范空問的基本概念。...
有界n線性運算元是映有界集的n線性運算元。n線性運算元的有界性與連續性是等價的。...... 有界n線性運算元是映有界集的n線性運算元。n線性運算元的有界性與連續性是等價...
所謂有界線性運算元空間,是指賦范線性空間X到賦范線性空間Y的有界線性運算元全體。...... 有界線性運算元是線性賦范空問的基本概念,是泛函分析中一種重要的運算元。...
對稱運算元A為本質自伴的充分條件有(其中條件1也是必要的):1、n-=n+,其中(n-=n+)為A的虧指數;2、A是半有界的,即存在實數r使對一切x∈𝓓(A)都有(Ax...
運算元還可分為有界的與無界的,線性的與非線性的等等類別。 [3] ...解決問題中的種種操作被稱為運算元(Operator)。 [4] 參考資料 1. 張晟. 下半...
非線性運算元又稱非線性映射,不滿足線性條件的運算元。泛函分析的研究對象主要是線性運算元及其特殊情況線性泛函。但是,自然界和工程技術中出現的大量問題都是非線性的。...
弗雷德霍姆運算元是可逆運算元的推廣。設T是希爾伯特空間H上的有界線性運算元,即T∈...,而dim (ker T)和dim(kerT*)中至少有一個有限,則稱T為半弗雷德霍姆運算元。...
設T是希爾伯特空間H上的稠定線性運算元,如果存在實數α,使得對於一切x∈𝓓(T)都有(Tx,x)≥α(x,x)(或(Tx,x)≤α(x,x))成立,就稱T是下半(或上半)...
強運算元拓撲(strong operator topology)是運算元空間中的又一種拓撲。從賦范線性空間X到賦范線性空間Y的有界線性運算元全體所成的賦范線性空間B(X→Y)中由半范族{...
弱運算元拓撲是運算元空間中的一種局部凸拓撲。設X,Y為賦范線性空間,𝓑(X,Y)為X到Y的有界線性運算元全體所成的賦范線性空間,𝓑(X→Y)中由半範數族(Px,f(...
m耗散運算元是運算元半群理論的一個重要概念。設X是一實巴拿赫空間,F:X→2X*是對偶映射。一個運算元A:D(A)⊂X→2X稱為耗散的,若對任意的x1,x2∈D(A),存在...
從復希爾伯特空間到復希爾伯特空間的有界線性運算元A的極分解,是將其正則分解為一個準等距變換和一個半正定運算元的乘積。矩陣的極分解被推廣為:如果A是一個有界線性...
彈性力學與流體力學等傾向於套用數學的問題.他首先把希爾伯特空間運算元的幾何理論套用到了偏微分運算元.1934年關於對稱橢圓運算元半有界擴張的工作,開始了二階橢圓方程研究...
《希爾柏脫空間運算元交換性質》一文,其專著《線性運算元譜理論》已由科學出版社出版,線上性拓撲數理論研究方面,他系統地建立了半賦范代數和局部有界代數的理論,其研究...
2.7 半線性橢圓邊值問題2.8 擬線性橢圓邊值問題第3章 一階發展方程3.1 引言3.2 線性有界運算元半群3.3 半群的無限小生成元3.4 解析半群...
