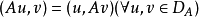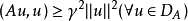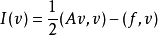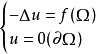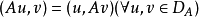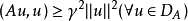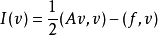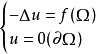正定運算元(positive definite operator)相應運算元方程可以化為變分問題的一類重要運算元。希爾伯特空間是歐幾里德空間的直接推廣。對希爾伯特空間及作用在希爾伯特空間上的運算元的研究是泛函分析的重要組成部分。
基本介紹
- 中文名：正定運算元
- 外文名：positive operator
- 領域：數學
- 性質：運算元
- 作用：將運算元方程轉化為變分方程
- 空間：希爾伯特空間
概念,運算元,變分問題,希爾伯特空間,泛函分析,
概念
正定運算元(positive definite operator)是相應運算元方程可以化為變分問題的一類重要運算元。設H是實希爾伯特空間，DA是H的一個線性稠密子集，A是DA→H的線性(不必有界)運算元。如果A是對稱的，即：
且存在正常數γ，使：
則稱A為DA上的正定運算元。對DA上的正定運算元A，求運算元方程Au=f(f∈H)的解u可以化成求泛函：
的解就是使泛函：
取極小值的極值函式。
運算元
運算元亦稱“算符”。邏輯、數學和物理學中對某些變換(映射)或運算的稱呼。例如在命題邏輯中，、∨、∧、→、↔等就分別稱為否定運算元、析取運算元、合取運算元、蘊涵運算元和等值運算元；其中是一個一元運算元(一元運算)，其餘四個都是二元運算元(二元運算)。又如在模態邏輯中通常把L(或□)和M(或◇)分別稱為必然運算元和可能運算元，或統稱它們為模態運算元。
變分問題
有關求泛函的極大值和極小值的問題。最早研究的重要變分問題有：
1.最速降線問題：給定不在同一鉛垂線上的兩點A和B，求出連結A和B的一條曲線使其具有這樣的性質：當質點受重力作用沿著這條曲線由A下滑至B時所需時間為最少。
2.短程線問題：求曲面φ(x，y，z)=0上所給二點間長度最短的曲線。這條最短曲線稱為短程線或測地線。
3.基本的等周問題：求長為一定的封閉曲線l，使其所圍的面積S為極大。
希爾伯特空間
希爾伯特空間是歐幾里德空間的直接推廣。對希爾伯特空間及作用在希爾伯特空間上的運算元的研究是泛函分析的重要組成部分。
設H是一個實的線性空間，如果對H中的任何兩個向量x和y，都對應著一個實數，記為(x，y)、滿足下列條件：
①對H中的任何兩個向量x，y，有(x，y)=(y，x);
②對H中的任何三個向量x、y、z及實數α、β，有(αx+βy，z)=α(x，z)+β(y，z);
③對H中的一切向量x，均有(x，x)≥0，且(x，x)=0的充分必要條件是x=0。則(x，y)稱為是H上的一個內積，而H稱為內積空間。
如果定義‖x‖=，則在‖0‖下，H構成一個線性賦范空間。
完備的內積空間稱為希爾伯特空間，希爾伯特空間的概念還可以推廣到複線性空間上。
歐幾里德空間是希爾伯特空間的一個重要特例，希爾伯特空間的另一個最重要的特例是L(G)，設G是n維歐幾里德空間中的一個有界閉域， 定義在G上的滿足⨜G|f(x)|dx<+∞的勒具格可測函式全體記為L(G)，在L2(G)中引入內積(f，g)=⨜Gf (x)g(x)dx，則L(G) 是一個希爾伯特空間，L(G)是實用中最重要和最常用的希爾伯特空間。
希爾伯特空間有許多與歐幾里德空間相似的性質，例如，在希爾伯特空間中，可以定義向量正交、正交和、正交投影的概念，柯西一許瓦茲不等式成立、勾股定理和投影定理成立。在可分希爾伯特空間中，存在著完全的標準正交系，希爾伯特空間中的任一向量可以依任一完全的標準正交系分解。
在泛函分析中，詳細地研究了希爾伯特空間自共軛運算元的理論，特別是自共軛運算元的譜理論，這一理論在經典數學的不少領域中有廣泛的套用。需要特別指出的是，自共軛運算元的譜理論，為量子力學的發展，提供了適合的工具。
理論數學、套用數學和物理中的許多問題，在希爾伯特空間中，可得到較好的處理，因此，希爾伯特空間成為泛函分析中最重要的和最常用的一類空間，它在許多其他數學分支、理論物理和現代工程技術理論中，也得到了廣泛的套用。
泛函分析
泛函分析是最近幾十年發展起來的具有高度抽象性和概括性的新的重要數學分支。它與抽象代數、拓撲學一起，構成了現代數學的三大基礎學科。泛函分析以無限維線性空間 (其中主要是無限維線性賦范空間)上的線性運算元和非線性運算元作為自己的主要研究對象，泛函分析的基本特點，在於它綜合地運用分析的、代數的和幾何(拓撲)的觀點和方法，以非常抽象的方式，統一地研究和處理經典數學各個領域中所出現的形式上非常不同的問題。
經典數學的許多領域，都是以作用在某種特殊函式類上的特定的運算作為自己研究對象的。例如，數學分析中的微分和積分運算，微分方程論中的常微分運算元和偏微分運算元，積分方程論中的積分運算元、古典變分學中的泛函等。在泛函分析中，各種各樣的函式類，被統一概括為線性空間 (一般是無窮維的)，而各種各樣的運算，則被統一概括為運算元 (線性的和非線性的)，泛函分析，正是以最一般的方式，研究作用在一般線性空間上的一般運算元。它所獲得的結論，對各種作用在特殊函式類上的特殊運算元都是適用的，從而具有高度的概括性、統一性和指導性，正是由於泛函分析的這種高度的抽象性和概括性，它才能廣泛地被利用。
