基本介紹
- 中文名:態射
- 外文名:morphism
- 數學定義:兩數學結構保持結構的過程的抽象
- 特點:態射不必是函式
- 套用學科:數學
- 所屬領域:集合論和拓撲學
定義


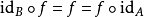

態射的類型
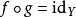



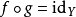
例子
- 在拓撲空間範疇,態射是連續函式,而同構稱為同胚。
- 在光滑流形範疇中,態射是光滑函式而同構稱為微分同胚。
- 函子可以視為小範疇的範疇中的態射。
- 在函子範疇中,態射是自然變換。



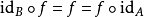

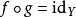



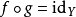
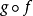
數學上,態射(morphism)是兩個數學結構之間保持結構的一種過程抽象。最常見的這種過程的例子是在某種意義上保持結構的函式或映射。例如,在集合論中,態射就是函式;...
在範疇論中,正規態射是一類可以自然地分解成單射與滿射的態射。使所有態射皆為正規態射的範疇稱為正規範疇。...
單位態射(unit morphism)亦稱可逆態射,是集合範疇中單位映射(可逆映射)概念的推廣。設f:A→B為範疇C中的態射,若有態射u使uf=εA(A上的恆等態射),則稱f...
單態射(monk morphism)是集合範疇Set中單射概念的推廣,它與滿態射是互為對偶的概念。...
射影空間是整體幾何最基本的研究對象之一。射影空間的概念最初產生於古典射影幾何。對於射影定理中的奇異情形(即有些直線相互平行的情形),為方便起見引入無窮遠...
弗羅貝尼烏斯態射(Frobenius morphism)是特徵p的概形上特有的態射。設k是一個特徵p>0的域。對任意一個k上的概形X,可以定義一個X到自身的態射FX:X→X,它...
平坦態射(flat morphism)是平坦模的推廣和相對化。平坦態射是開映射,而且是等維數的(即對於s∈S的鄰域,f的纖維有相同維數)。...
仿射態射(affine morphism)仿射概形的相對化.設有概形間的態射:f: x-}s,使得s中任何仿射開子概形的原像都是仿射概形,這時x稱為仿射s概形.仿射態射當然...
正常態射(proper morphism)完備簇的相對化,就是概形間的分離、絕對閉、有限型態射。...
零態射(zero morphism)是有零對象的範疇中的一類特殊態射。許多常見範疇,如群範疇、環範疇、環模疇等,將它們的零同態概念抽象出來即得零態射的概念,它在範疇論...
《態射與範疇:比較與轉換》這本書主要闡述了有關生物和智力之形式的一般理論, 並指出這種理論是建立在態射和範疇這兩種互相協調的數學工具的基礎之上的。...
平展態射(etale morphism)一種重要的光滑態射.代數簇或概形間相對維數等於。的光滑態射,它也可以等價地定義為概形間的不分歧平坦態射.當X和Y都是光滑簇(即...
光滑態射是光滑概形的相對化,也可看成是非異代數簇的族。設f:X→S是有限型態射,若f是平坦態射,並且對任一個點s∈S,纖維f-1(s)是剩餘域k(s)上的光滑...
態射核(kernel of a morphism)群論中同態核概念的推廣(不過在群論中同態核是一個正規子群,而在群範疇中則是指此正規子群及其在群中的嵌入同態).態射的核是...
不分歧態射(unramified morphism)代數數論中的不分歧擴張的推廣.不分歧態射f:X-}S是概形間的局部有限型態射,使得對每個:ES都有X}=日Spec k,其中k是:的剩餘...
擬射影態射(quasi-projective morphism)擬射影簇的推廣及相對化。...... 擬射影態射(quasi-projective morphism)擬射影簇的推廣及相對化。若g:Y->S是射影態...
態射上核(cokernel of a morphism)群論中同態的上核概念的推廣(不過,在群論中同態的上核是指一個商群,而在群範疇中是指此商群及群到此商群的滿同態).態...
本書主要闡述了有關生物和智力之形式的一般理論, 並指出這種理論是建立在態射和範疇這兩種互相協調的數學工具的基礎之上的。態射是建立在兩個集合之間關係系統之...
雙態射(bimorphism)集合範疇中雙射概念的推廣.在範疇中同時為單態射與滿態射的態射稱為雙態射.換言之,雙態射即滿足左可消與右可消的態射.在群範疇與阿貝爾...
讓C成為一個類,H是C的一類態射;如果從X到H的內射對象中存在一個H態射的話,那么對於C類中的每個對象X都有充足的H態射。並且,H通常是單態的類,並且對於C...
加性範疇(additive category)亦稱加法範疇。是一種常用範疇。範疇是範疇論的基本概念之一。例如,以一切集合作對象,以集合映射作態射,則得集合範疇Set(簡稱集範疇)...
每一範疇都可由其物件、態射和態射複合來表示。1.所有集合的範疇Set,其態射為集合間的函式,而態射複合則為一般的函式複合。(下列皆為具體範疇的例子,即在Set...
例如,設f:X→S是一個態射,若對角浸入X→X×SX是閉態射,則稱f是分離態射;若存在S的一個仿射開覆蓋{Ui}={Spec Bi},使得每個f(Ui)都有一個有限仿射開...
在抽象代數(abstract algebra)中,同構(isomorphism)指的是一個保持結構的雙射(bijection)。在更一般的範疇論語言中,同構指的是一個態射,且存在另一個態射,使得...
.論文“有滿單分解態射的 Moore-Penrose 逆” 1994 年獲湖北省科協優秀論文二等 獎.論文“ P- 除環上子空間的交與和及其維數” 1993 年獲湖北省數學會代數...
