基本介紹
- 中文名:單位態射
- 外文名:unit morphism
- 別稱:可逆態射
- 簡介:集合範疇中單位映射概念的推廣
- 所屬學科:數學(範疇論)
- 相關概念:單態射,滿態射等
定義







相關概念
等價態射






單態射

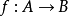


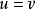



滿態射
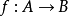

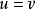


















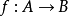


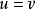



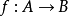

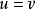



單位態射(unit morphism)亦稱可逆態射,是集合範疇中單位映射(可逆映射)概念的推廣。設f:A→B為範疇C中的態射,若有態射u使uf=εA(A上的恆等態射),則稱f...
態射核(kernel of a morphism)群論中同態核概念的推廣(不過在群論中同態核是一個正規子群,而在群範疇中則是指此正規子群及其在群中的嵌入同態).態射的核是...
態射上核(cokernel of a morphism)群論中同態的上核概念的推廣(不過,在群論中同態的上核是指一個商群,而在群範疇中是指此商群及群到此商群的滿同態).態...
單態射(monk morphism)是集合範疇Set中單射概念的推廣,它與滿態射是互為對偶的概念。...
5.若I是一個集合,“在 上的具體範疇”會是個小範疇,其物件為的元素,而態射則只有單位態射。當然,其態射複合的公理是必然滿足的。...
加性範疇(additive category)亦稱加法範疇。是一種常用範疇。範疇是範疇論的基本概念之一。例如,以一切集合作對象,以集合映射作態射,則得集合範疇Set(簡稱集範疇)...
在數學中,一個範疇C的子範疇(subcategory)是一個範疇S,其物件為C內的物件,態射為C內的態射,且有相同的單位態射與態射複合。直觀上來看,C的子範疇是一個...
。換言之,函子會保持單位態射與態射的複合。一個由一範疇映射至其自身的函子稱之為“自函子”。函子例子 編輯 常函子(Constant functor):把 中的所有對象都...
子對象是子代數系概念的推廣。它是商對象的對偶概念。設 A,B 為範疇 𝒞 的兩個對象,若有單態射 i:A→B,則稱 A 為 B 的子對象。例如在環範疇中,環 ...
伴隨函子單位泛態射形式定義 給定兩個函子F:C→D與G:D→C,自然變換η:1c→GF。F┤G稱為伴隨對,若對任意C∈C,D∈D,f:C→GD,存在惟一的g:FC→D,...
