基本介紹
- 中文名:子範疇
- 外文名:subcategory
- 學科:數理科學
- 領域:範疇論
定義
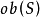
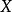
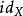


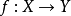
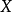
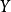
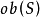

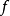
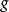
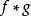


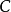
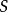
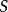
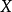
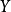

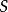
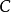
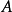

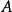
內嵌
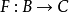
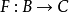

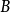
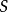
子範疇類型
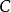
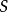
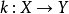
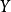
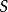

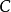
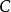
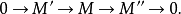

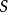
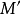
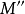
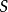
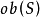
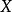
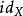


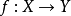
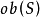

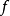
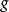
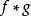


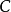
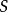
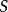
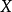
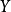

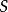
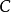
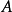

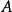
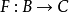
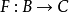
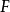
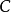
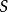

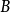
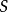
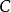
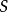
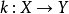
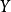
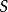

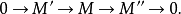

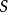
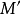
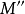
在數學中,一個範疇C的子範疇(subcategory)是一個範疇S,其物件為C內的物件,態射為C內的態射,且有相同的單位態射與態射複合。直觀上來看,C的子範疇是一個...
全子範疇(full subcategory)是一種特殊的子範疇,設D為C的子範疇,若子範疇定義中的條件HomD(A,B)⊆HomC(A,B)改為HomD(A,B)=HomC(A,B),則稱D為C...
小範疇是一種重要的常用範疇。一個範疇的全體對象一般地只成類而不是集合,當其對象類是一個集合時就稱此範疇為小範疇。例如,R為實數集,將實數作為對象,當a≤...
塞爾子範疇(Serre subcategory)阿貝爾範疇的一種子範疇.它在同調代數等學科中有重要套用,也是定義商範疇的基礎概念.設留為阿貝爾範疇,少為留的全子範疇且滿足:對留...
具體範疇(concrete category)一種常用的重要範疇.對象都是集合的範疇稱為具體範疇,可以看成r-,f'et(集合範疇)的子範疇,代數學中的常用範疇都是具體範疇.用函子...
局部小範疇(ocall small category)亦稱良效範疇一種特殊的範疇.若省是一個範疇,其任意對象A的子對象的等價類(同構類)都是集合,則稱為局部小範疇.由集合論的ZF...
子對象是子代數系概念的推廣。它是商對象的對偶概念。設 A,B 為範疇 𝒞 的兩個對象,若有單態射 i:A→B,則稱 A 為 B 的子對象。例如在環範疇中,環 ...
在範疇論中,米田引理斷言一個對象X的性質由它所表示的函子 Hom(X,-)或Hom (-,X)決定。此引理得名於日本數學家暨計算機科學家米田信夫。...
套用範疇論時,關鍵是先搞清研究問題以什麼作對象,以什麼作態射(參見“範疇”).研究不同範疇之間的關係時,關鍵在於找到適當的函子。範疇論的核心是函子理論。艾倫...
其數目不足裂變中子總數的1%;其能量分布也是連續譜,平均能量在1MeV以下。緩發性中子與核反應產生的瞬發中子相比能量能級要小很多,大部分屬於熱中子範疇。[1] ...
冷壓端子包括電子連線器,空中接頭。是用於實現電氣連線的一種配件產品,工業上劃分為連線器的範疇。...
