基本介紹
- 中文名:函子
- 外文名:functor
- 領域:範疇論
- 學科:數學
簡介
定義





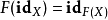


例子

















雙函子與多函子
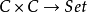

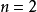
性質

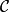
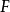















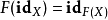



















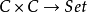

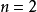

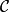
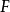










在範疇論中,函子(functor)是範疇間的一類映射,通俗地說,是範疇間的同態。...... 在範疇論中,函子(functor)是範疇間的一類映射,通俗地說,是範疇間的同態。...
可表示函子,兩範疇間的一類特殊函子,有泛元素的函子。...... 可表示函子,兩範疇間的一類特殊函子,有泛元素的函子。中文名 可表示函子 外文名 representable...
函子是範疇間的一類特殊映射。有些問題中需研究兩個範疇間的聯繫或通過這種聯繫由一個範疇的性質來推斷另一範疇的性質,這就引出函子的概念。函子可看成範疇間的...
表示函子(representative functor)是範疇論里的概念,指從任意範疇到集合範疇的一種特殊函子。這種函子將抽象的範疇表達成人們熟知的結構(即集合與函式),從而使得對...
在範疇論中,正合函子(或譯作恰當函子)是保存有限極限的函子。在阿貝爾範疇中,這就相當於保存正合序列的函子。...
在同調代數中,阿貝爾範疇間的某類函子可以“求導”,以獲得相應的導出函子。此概念可以融貫數學中許多領域裡的具體構造。導出函子包括左導出函子和右導出函子。...
右導出函子是一類重要的函子,左導出函子的對偶概念,是由函子T導出的新函子。...... 右導出函子是一類重要的函子,左導出函子的對偶概念,是由函子T導出的新...
可表函子是在數學中範疇論里的概念,指從任意範疇到集合範疇的一種特殊函子。這種函子將抽象的範疇表達成人們熟知的結構(即集合與函式),從而使得對集合範疇的了解...
包含函子(inclusion functor)包含映射的推廣.它一種嵌人函子.若若‘為範疇留的子範疇,可用顯見方式定義一個函子I:}(使I(A)=A,I(f)=f),則稱這個函子I...
共尾函子(final functor)是代數K理論中定義纖維範疇時用到的一類重要函子。它是一類特殊的保積函子。設(C,⊥),(D,⊥)為帶積範疇,F:C→D為保積函子。若...
對偶函子(dual functor)是對偶範疇間的一個顯見函子。即刻畫範疇C與C°間關係的一個標準函子。函子是範疇間的一類特殊映射。有些問題中需研究兩個範疇間的...
忠實函子(faithful functor)亦稱信守函子,是全函子的對偶概念。設F:C→D為函子,若τ,σ∈HomC(A,B),τ≠σ,必F(τ)≠F(σ),則稱F為C到D的忠實函...
二元函子(bifunctor)是範疇論以及同調代數、代數幾何等學科中常用的函子。若C1,C2,C為三個範疇,則從C1,C2的積範疇C1∏C2到C的函子稱為二元函子,同調代數中...
函子自然變換是處理函子之間關係的一個重要概念,由它可得出有用的可換圖。...... 函子自然變換是處理函子之間關係的一個重要概念,由它可得出有用的可換圖。...
嵌入函子(embedding functor)一類特殊的忠實函子.關於態射及對象都是單射的函子,設F為函子,若aEHom}=(A,B),必F =F (Q),則稱F為子函子,即變不同對象...
滿單函子(epi-mono functor)一種常用的函子.它在研究分次模範疇時有重要價值.給定G分次環R.在範疇R-gr和R-mod間有四個常用的函子: 1·誘導函子Ind : ...
遺忘函子(forgetful functor)亦稱忘卻函子或基礎函子一類重要的函子.在拓撲空間範疇的研究中有時只需考慮其中的集合性質,即,將其每個對象看做一個集合(基礎集),...
反變Hom函子(contravariant func-for Hom in category theory)亦稱反變態射函子或第二表示函子.是範疇論中的重要函子之一,也是同調代數中最基本的函子之一設留...
Hom函子(functor Hom)是模範疇間最重要的函子之一。...... Hom函子(functor Hom)是模範疇間最重要的函子之一。對左A模M,N,模同態全Hom函子(functor Hom)...
上同調函子是一種重要的函子,指由上復形的範疇到模範疇的函子。範疇A-Cocomp,它的對象是環 A 上所有上復形,態射是復形的平移,把這個範疇稱為上復形的...
U對偶函子(U-duality functor)模範疇對偶性中的重要函子。...... U對偶函子(U-duality functor)模範疇對偶性中的重要函子。U對偶函子(U-duality functor)模範...
正式定義為,給定兩個範疇C與D,一個範疇等價包括函子F:C→D,函子G:D→C,以及兩個自然同構 ε:FG→ID與η:IC→GF。這裡FG:D→D與GF:C→C分別為F與G...
實際上,即是定義了一個“範疇和函子”的範疇,其元件為範疇,(範疇間的)態射為函子。經由研究範疇和函子,不只是學習了一類數學結構,及在其之間的態射;還學習...
