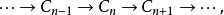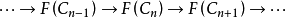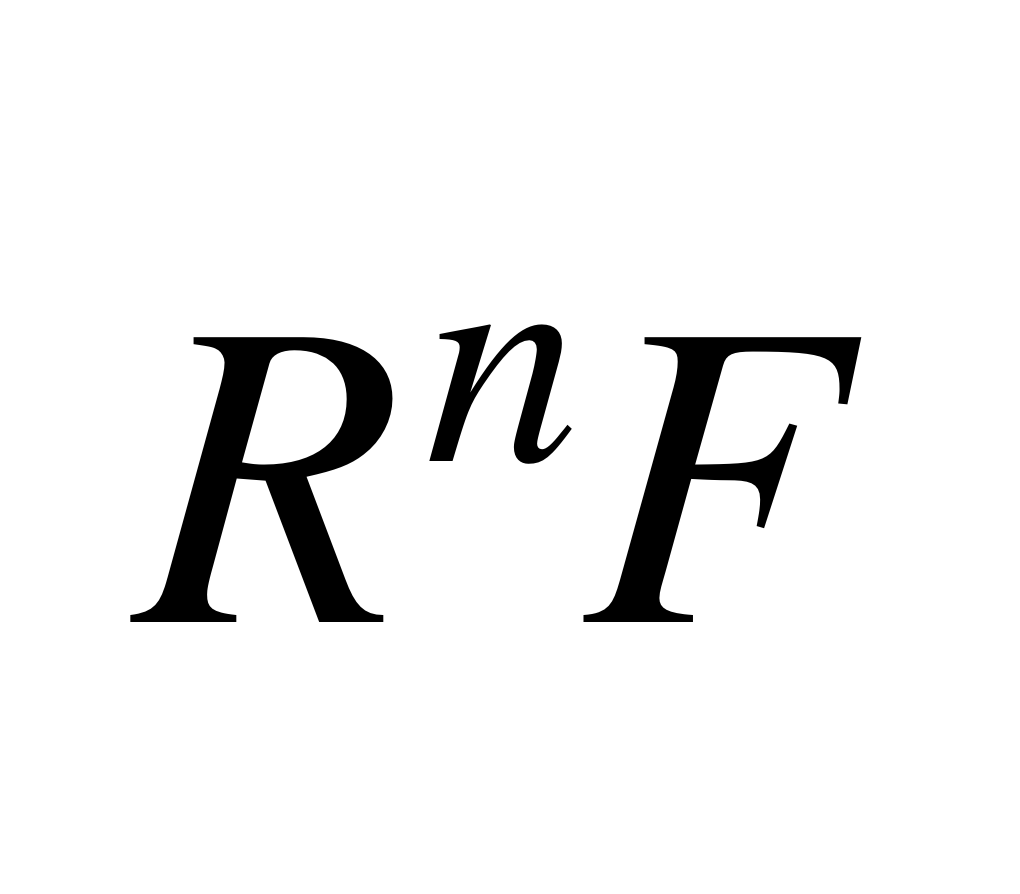右導出函子是一類重要的函子,左導出函子的對偶概念,是由函子T導出的新函子。
基本介紹
- 中文名:右導出函子
- 外文名:right derived functor
定義,左導出函子,函子Ext,正合函子,
定義
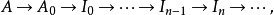
得到鏈復形
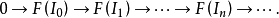
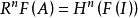
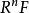
左導出函子
設 F :𝓐→𝕭是交換範疇的右正合加性函子,A有足夠的投射對象。設A ∈ A,F作用於A的投影分解
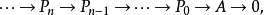
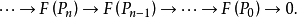
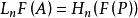
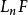
函子Ext
(functor Ext)設R為環,R模範疇有足夠多的投射對象和內射對象。對任意R模M,函子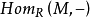 為左正合的,其右導出函子記為
為左正合的,其右導出函子記為 ,稱為函子Ext。
,稱為函子Ext。
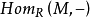

正合函子
(exact functor)設𝗖,𝕯為交換範疇,F :𝗖 →𝕯為加性函子。如果對 C 中每個正合列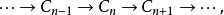 F作用後得到的序列
F作用後得到的序列