左導出函子

在同調代數中，阿貝爾範疇間的某類函子可以“求導”，以獲得相應的導出函子。此概念可以融貫數學中許多領域裡的具體構造。導出函子包括左導出函子和右導出函子。

基本介紹

• 中文名：左導出函子
• 外文名：Left Derived functor
• 領域：數學

簡介

在同調代數中，阿貝爾範疇間的某類函子可以“求導”，以獲得相應的導出函子。此概念可以融貫數學中許多領域裡的具體構造。

考慮導出函子的原始目的是從一個短正合序列造出一個長正合序列。具體言之：給定兩個阿貝爾範疇 ，及其間的加法函子 。假設 為左正合函子，換言之，對 中的任一短正合序列

下列序列是正合的：

構造與初步性質

右導出函子

今假設 中有充足的內射元。設 ，根據假設，存在內射分解：

取函子 ，得到上鏈復形：

定義為其第個上同調群，特別是有。注意到兩點：

由於任兩個內射分解彼此同倫等價，函子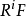在同構的意義下是明確定義的。

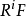
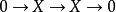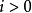若是內射對象，取平凡分解，可知當時有。

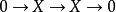
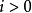
左導出函子

左導出函子的建構與右導出函子對偶。設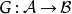為右正合加法函子，並假設有充足的射影元。對任一對象，取一射影分解：

取函子，得到鏈復形：

定義為其第個同調群，其性質類似右導出函子。

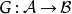
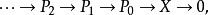
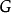
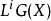
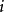
逆變函子的情形

對於逆變函子也能定義導出函子，此時的導出函子也是逆變函子。較有系統的方法是利用反範疇的概念。

長正合序列

對於右導出函子的情形，任一短正合序列給出長正合序列：

對於左導出函子，相應的長正合序列形如：

此外，這些長正合序列在下述意義下是“自然”的：

• 短正合列之間的態射導出長正合序列間的態射。
  
• 函子間的自然變換導出長正合序列尖的態射。
  

這些性質是蛇引理的推論。

套用

層上同調：對拓撲空間，考慮其上的阿貝爾群層構成的範疇，它有充足的內射元。整體截面函子是左正合函子，相應的右導出函子即層上同調函子。

平展上同調：平展上同調用於概形上的另一種上同調理論。

Ext函子：設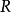為環，考慮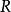-模範疇，它有充足的內射元及射影元。對任一-模，函子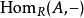為左正合的，其右導出函子記為。

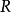
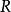
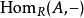
Tor函子：同樣考慮-模範疇，對任一-模，函子為右正合的，其左導出函子記為。

群上同調：設為群。所謂-模是指被作用的阿貝爾群，-模範疇可以理解為-模範疇。對任一-模，定義，這是一個左正合函子，其右導出函子即群上同調函子。

推廣

現代的導範疇理論為導出函子提供了一套較廣的框架。