概形(scheme)代數幾何的基本研究對象。它實際上就是一個局部同構於仿射概形的局部環空間.更精確地,概形(X,Ox)是一個環空間,其拓撲空間X有一個開覆蓋{X,. },.E},使得(X;,Ox}X)同構於仿射概形Spec T (X; , Ox(這樣的覆蓋稱為仿射開覆蓋)。
基本介紹
- 中文名:概形
- 外文名:scheme
- 學科:數理科學
- 領域:幾何學
定義

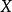
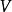

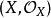
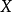


歷史
簡介
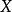
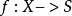
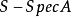
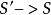
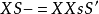
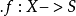
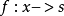

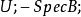


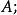

概形(scheme)代數幾何的基本研究對象。它實際上就是一個局部同構於仿射概形的局部環空間.更精確地,概形(X,Ox)是一個環空間,其拓撲空間X有一個開覆蓋{X,. },.E},使得(X;,Ox}X)同構於仿射概形Spec T (X; , Ox(這樣的覆蓋稱為仿射開覆蓋)。

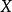
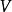

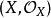
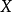


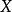
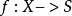
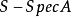
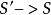
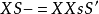
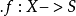
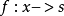

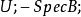


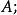

概形(scheme)代數幾何的基本研究對象。它實際上就是一個局部同構於仿射概形的局部環空間.更精確地,概形(X,Ox)是一個環空間,其拓撲空間X有一個開覆蓋{X,. ...
這是概形論術語。欲知代數幾何中概形的簡介,請見條目仿射概形、射影空間、層及概形。本條目旨在列出概形論中的基本技術定義與性質。...
概形是代數幾何的基本研究對象。它實際上就是一個局部同構於仿射概形的局部環空間。更精確地,概形(X,OX)是一個環空間,其拓撲空間X有一個開覆蓋{Xi}i∈I,...
希爾伯特概形(Hilbert scheme)一種特殊概形.設T是一個諾特概形,X是T上的射影概形,CT是所有局部諾特T概形的範疇.定義一個從CT到集合範疇的函子Hilbx/二如下...
在代數幾何中,一個概形S上的群概形G是範疇SchS中的群對象,具體定義請參見正文。...... 在代數幾何中,一個概形S上的群概形G是範疇SchS中的群對象,具體定義...
光滑概形(smooth scheme)是光滑代數簇概念的推廣。設X是域k上的有限型概形,若k'是k的代數閉包,X的基擴張Xk'是正則概形,則稱X是光滑概形。一個域的最大...
皮卡概形是與射影光滑代數簇相關聯的一個群概形。皮卡概形是光滑代數簇X的皮卡簇。...... 皮卡概形是光滑代數簇X的皮卡簇𝕭(X)的概念在概形理論框架內的自...
諾特概形(Noetherian scheme)是諾特環的推廣。若一個概形X有一個由諾特環的譜所構成的有限仿射開覆蓋,則稱X是諾特概形。概形是代數幾何的基本研究對象。它實際...
子概形(subscheme)開子概形、閉子概形與一般子概形的統稱.概形(X ,Ox)的開子概形就是一個概形(U,Ou),其中拓撲空間U是X的開子集,結構層Or; -O川二...
既約概形(reduced scheme)代數簇的推廣.若一個概形(X,O襯的每一個點x的局部環fix,二都不含非零冪零元,則稱X是既約概形.任意一個概形(X,Ox)都含有一...
正則概形(regular scheme)光滑代數簇的推廣.若概形(X,Ox)在每個點xEX的局部環fix.,都是正則局部環,則稱為正則概形.若X是代數閉域上的代數簇,則正則性和非...
阿貝爾S概形(Abelian S scheme)纖維都是阿貝爾簇的光滑S群概形.一個光滑的S群概形,它的纖維都是阿貝爾簇.阿貝爾S概形也可以等價地定義為具有幾何連通纖維的正常...
《群概形及其作用論》是2018年出版的圖書,作者是李克正。...... 群概形是代數幾何與算術代數幾何的重要課題。本書內容不僅包括群概形的基本理論,而且包括其他一些...
代數空間(algebraic space)代數簇和概形概念的推廣。代數空間是阿廷(Artin,E.)引入的,主要目的是為了彌補概形範疇關於許多取商的函子不封閉的缺陷。代數空間關於...
該書把代數幾何的基礎系統地建立在概形的概念之上。這部著作被視為現代代數幾何的奠基之作和基本參考書。書名 代數幾何原理 又名 代數幾何基礎 作者 格里菲思(...
弗羅貝尼烏斯態射(Frobenius morphism)是特徵p的概形上特有的態射。設k是一個特徵p>0的域。對任意一個k上的概形X,可以定義一個X到自身的態射FX:X→X,它...
霍普夫代數以數學家海因茨·霍普夫命名,此類結構廣見於代數拓撲、群概形、群論、量子群等數學領域。中文名 霍普夫代數 外文名 Hopf algebra 本質 一類雙代數 目錄...
扎里斯基拓撲(Zariski topology)是代數簇與概形的研究中使用的一種拓撲。扎里斯基拓撲往往用指定空間中的閉子集的方式來定義。仿射空間A中的扎里斯基閉集就是某一族...
本書同時介紹兩類代數群:線性代數群和Abel概形,全書分為三篇。第一篇介紹定義在代數閉域上的線性代數群,主要討論根繫結構,並且討論線性代數群的Galois上同調理論...
由於概形無非是交換環譜的黏合,交換代數遂成為研究概形局部性質的主要語言。中文名 交換代數 外文名 commutative algebras 屬於 交換環的一門代數學科 套用學科 ...
光滑態射是光滑概形的相對化,也可看成是非異代數簇的族。設f:X→S是有限型態射,若f是平坦態射,並且對任一個點s∈S,纖維f-1(s)是剩餘域k(s)上的光滑...
