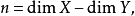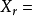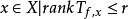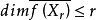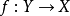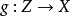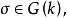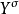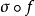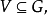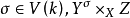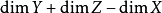基本介紹
- 中文名:光滑態射
- 外文名:smooth morphism
- 所屬學科:數學
- 相關概念:光滑概形、平展態射等
基本介紹,相關概念與性質,
基本介紹
光滑態射是光滑概形的相對化,也可看成是非異代數簇的族。設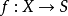 是有限型態射,若
是有限型態射,若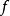 是平坦態射,並且對任一個點
是平坦態射,並且對任一個點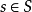 ,纖維
,纖維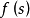 是剩餘域
是剩餘域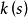 上的光滑概形,則稱
上的光滑概形,則稱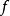 是光滑態射,X稱為光滑S概形,仿射S空間
是光滑態射,X稱為光滑S概形,仿射S空間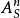 和射影S空間
和射影S空間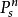 都是光滑S概形。當X和S有相同維數時平展態射是光滑態射,反之,光滑態射
都是光滑S概形。當X和S有相同維數時平展態射是光滑態射,反之,光滑態射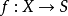 總可以局部地分解為平展態射
總可以局部地分解為平展態射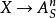 與投影
與投影 的合成。
的合成。
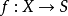
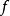
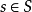
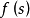
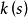
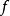
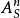
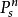
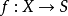
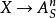

相關概念與性質
光滑態射的概念是域上非異簇概念的一種相對形式。為簡便起見,假定所有概型都是在域k 上的有限型。
定義
k上有限型概型間的態射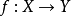 相對維度n光滑,如果
相對維度n光滑,如果
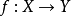
(1) f為平坦;
(2) 如果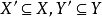 為不可約分支使
為不可約分支使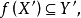 則
則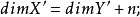
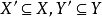
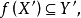
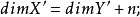
(3) 對每個點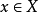 (閉與否),
(閉與否),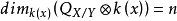 。
。
命題1
(a) 開浸沒相對維數0光滑。
(b) 底變換:設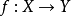 相對維數n光滑,
相對維數n光滑,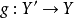 為任意態射,則由底擴張得到的射
為任意態射,則由底擴張得到的射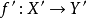 也相對維數n 光滑。
也相對維數n 光滑。
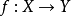
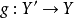
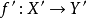
(c) 複合: 若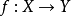 相對維數n光滑,
相對維數n光滑,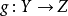 具相對維數m光滑,則
具相對維數m光滑,則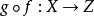 具相對維數
具相對維數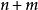 光滑。
光滑。
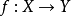
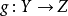
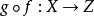
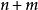
(d) 積:若X及Y 對Z光滑,分別具有相對維數n及m,則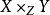 相對維數
相對維數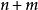 在Z 上光滑。
在Z 上光滑。
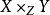
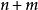
定理1
設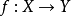 為k上有限型概型間態射,則
為k上有限型概型間態射,則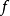 具相對維數n光滑,若且唯若:
具相對維數n光滑,若且唯若:
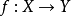
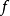
(1)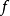 平坦,且
平坦,且
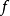
(2) 對每個點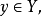 令
令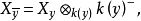 其中
其中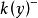 是
是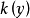 的代數閉包,則
的代數閉包,則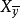 為n維勻維且正則,(這時稱“
為n維勻維且正則,(這時稱“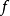 的纖維為幾何正則,具有勻維n")
的纖維為幾何正則,具有勻維n")
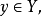
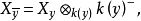
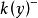
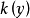
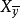
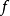
命題2
(i) 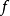 為具有相對維數n 且光滑;
為具有相對維數n 且光滑;
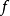
(ii)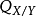 為X上n 秩的局部自由層;
為X上n 秩的局部自由層;
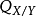
(iii)對每個閉點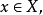 Zariski切空間上的誘導映射
Zariski切空間上的誘導映射 為滿。
為滿。
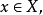

性質1 (一般光滑性) 設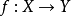 為特徵0代數閉域k上簇間的射,並設X為非異,則存在非空開子集
為特徵0代數閉域k上簇間的射,並設X為非異,則存在非空開子集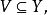 使
使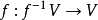 為光滑。
為光滑。
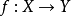
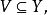
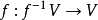
注意 :任意群簇均為齊性空間,只要讓它以左乘積作用於自己。
性質2(Bertini)設X 是特徵0的代數閉域k 上的非異射影簇,令b是個無基點線性系,則b中幾乎每個元,將它看作X的閉子概型時,都是非異的(但可能是可約的)。