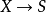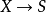平坦態射(flat morphism)是平坦模的推廣和相對化。平坦態射是開映射,而且是等維數的(即對於s∈S的鄰域,f的纖維有相同維數)。
基本介紹
- 中文名:平坦態射
- 外文名:flat morphism
- 套用學科:數學術語
- 範疇:數理科學
- 定義:平坦模的推廣和相對化
- 涉及:平坦模
概述,定理及引理,
概述
平坦態射(flat morphism)是平坦模的推廣和相對化。設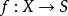 是概形的態射,若對於任意的點
是概形的態射,若對於任意的點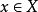 ,局部環
,局部環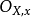 是平坦
是平坦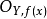 環,則稱
環,則稱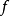 是平坦態射,X稱為平坦S概形。直觀上看,有限型平坦態射相當於代數簇的連續族。平坦態射是開映射,而且是等維數的(即對於
是平坦態射,X稱為平坦S概形。直觀上看,有限型平坦態射相當於代數簇的連續族。平坦態射是開映射,而且是等維數的(即對於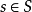 的鄰域,
的鄰域,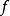 的纖維有相同維數)。若平坦態射
的纖維有相同維數)。若平坦態射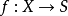 又是滿的,則
又是滿的,則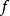 稱為忠實平坦的。
稱為忠實平坦的。
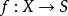
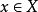
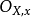
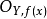
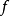
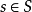
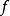
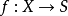
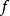
定理及引理
平坦性是一個不很直觀的概念:一個環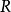 上的模稱為平坦模,如果對任意
上的模稱為平坦模,如果對任意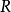 -模的單同態
-模的單同態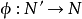 ,誘導同態
,誘導同態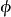 ⓧ
ⓧ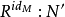 ⓧ
ⓧ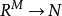 ⓧ
ⓧ 是單同態。設
是單同態。設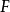 為一個代數集
為一個代數集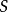 上的
上的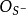 模層,若任一點
模層,若任一點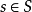 上的莖
上的莖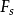 是
是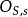 上的平坦模,則稱
上的平坦模,則稱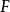 在
在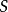 上是平坦的。一個代數集的態射
上是平坦的。一個代數集的態射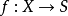 稱為平坦的,如果對任意
稱為平坦的,如果對任意 ,
,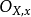 是平坦
是平坦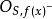 模(此時亦稱
模(此時亦稱 在
在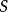 上平坦)。
上平坦)。
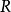
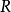
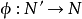
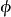
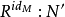
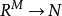

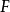
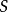
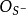
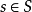
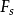
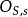
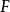
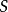
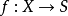

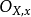
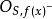

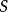
引理:設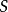 為代數閉域
為代數閉域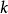 上的擬射影代數集,
上的擬射影代數集,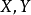 為
為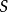 上的代數集(即給定了態射
上的代數集(即給定了態射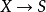 和
和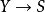 )。
)。
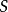
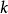
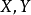
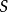
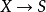
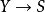
(1)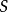 上的可逆層是平坦的。
上的可逆層是平坦的。
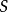
(2)開嵌入是平坦態射。
(3)平坦態射的合成是平坦態射。
(4)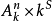 和
和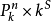 在
在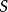 上平坦。
上平坦。
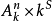
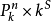
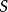
(5)若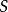 和
和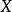 都是仿射的,其函式環分別為
都是仿射的,其函式環分別為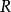 、
、 ,則
,則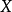 在
在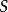 上平坦若且唯若
上平坦若且唯若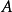 為平坦
為平坦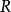 -模。
-模。
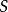
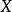
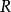

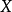
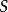
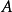
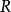
(6)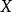 在
在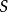 上平坦若且唯若
上平坦若且唯若 有一個開覆蓋
有一個開覆蓋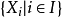 ,其中每個
,其中每個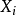 在
在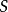 上平坦。
上平坦。
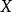
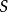

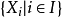
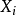
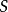
(7)若態射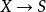 平坦則態射
平坦則態射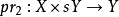 平坦(簡言之“基變換保持平坦性”)。
平坦(簡言之“基變換保持平坦性”)。
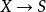
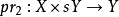
(8)設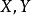 在
在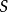 上平坦,
上平坦,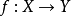 為
為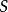 -態射。若對任一點
-態射。若對任一點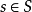 ,
,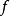 在
在 上的纖維
上的纖維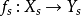 平坦,則
平坦,則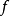 平坦。
平坦。
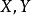
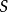
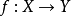
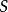
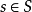
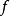

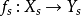
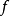
(9)設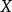 在
在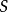 上平坦,
上平坦, 為閉嵌入,其理想層為
為閉嵌入,其理想層為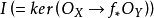 。若
。若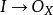 在任意點
在任意點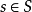 上的纖維
上的纖維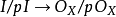 是單射,則
是單射,則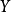 在
在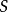 上平坦。
上平坦。
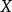
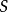

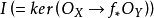
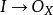
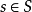
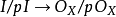
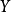
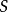
(10)若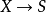 是平坦滿射且
是平坦滿射且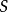 是連通的,則
是連通的,則 在
在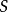 上的所有纖維具有相同的維數。
上的所有纖維具有相同的維數。
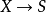
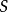

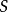
(11)若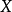 在
在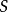 上是有限的,則
上是有限的,則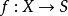 平坦若且唯若
平坦若且唯若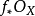 是局部自由
是局部自由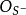 模層。
模層。
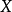
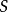
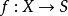
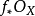
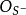
(12)若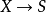 平坦則
平坦則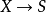 是開映射。
是開映射。