算術曲面(arithmetic surface)算術代數幾何里的重要研究對象。
設R是一個戴德金環,F是R的分式域,記Y=Spec R,若X是一個Y整概形,使得X->Y是一個正常、平坦態射,並且一般纖維X F.是一條非奇異曲線,則稱X為算術曲面.算術曲面最簡單的例子就是費馬曲面,即取
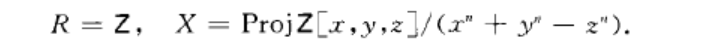
.這時Y=specz是與整數環對應的算術曲線,x就相當於Y上的一個纖維化曲面.因此研究算術曲面的目的之一就是為了解決費馬猜想.
算術曲面(arithmetic surface)算術代數幾何里的重要研究對象。
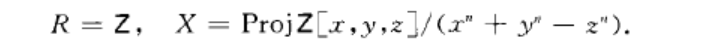
算術曲面(arithmetic surface)算術代數幾何里的重要研究對象。...... 算術曲面(arithmetic surface)算術代數幾何里的重要研究對象。設R是一個戴德金環,F是R的分式域,...
定義在曲面上的函式或向量值函式關於該曲面的積分。曲面積分一般分成第一型曲面積分和第二型曲面積分。第一型曲面積分物理意義來源於對給定密度函式的空間曲面,計算...
定義在曲面上的函式關於該曲面的積分。第一型曲線積分物理意義來源於對給定密度函式的空間曲面,計算該曲面的質量。...
旋轉曲面,也稱迴轉曲面,是一類特殊的曲面,它是一條平面曲線繞著它所在的平面上一條固定直線旋轉一周所生成的曲面。該固定直線稱為旋轉軸,該旋轉曲線稱為母線。...
曲面細分,英文稱Tessellation,如果直譯的話應該譯作“鑲嵌化處理技術”。由ATI開發,微軟採納後將其加入DirectX 11,成為DirectX 11的組成部分之一。由於這種技術廣泛的...
第二型曲面積分是關於在坐標面投影的曲面積分,其物理背景是流量的計算問題。第二型曲線積分與積分路徑有關,第二型曲面積分同樣依賴於曲面的取向,第二型曲面積分與...
