定義在曲面上的函式或向量值函式關於該曲面的積分。曲面積分一般分成第一型曲面積分和第二型曲面積分。
第一型曲面積分物理意義來源於對給定密度函式的空間曲面,計算該曲面的質量。第二型曲面積分物理意義來源對於給定的空間曲面和流體的流速,計算單位時間流經曲面的總流量。
基本介紹
- 中文名:曲面積分
- 外文名:Surface Integral
- 屬性:數學概念
- Σ:積分曲面
- dS:面積微元
第一型





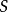



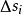





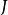
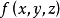


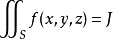

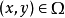

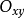






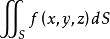



第二型













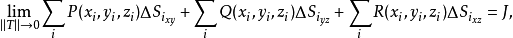





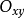
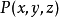







定義在曲面上的函式或向量值函式關於該曲面的積分。曲面積分一般分成第一型曲面積分和第二型曲面積分。
第一型曲面積分物理意義來源於對給定密度函式的空間曲面,計算該曲面的質量。第二型曲面積分物理意義來源對於給定的空間曲面和流體的流速,計算單位時間流經曲面的總流量。





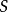



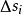





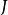
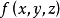


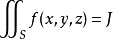

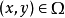

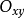






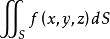
















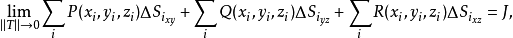
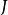
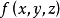




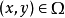

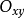
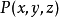






定義在曲面上的函式或向量值函式關於該曲面的積分。曲面積分一般分成第一型曲面積分和第二型曲面積分。第一型曲面積分物理意義來源於對給定密度函式的空間曲面,計算...
定義在曲面上的函式關於該曲面的積分。第一型曲線積分物理意義來源於對給定密度函式的空間曲面,計算該曲面的質量。...
第二型曲面積分是關於在坐標面投影的曲面積分,其物理背景是流量的計算問題。第二型曲線積分與積分路徑有關,第二型曲面積分同樣依賴於曲面的取向,第二型曲面積分與...
積分輪換對稱性是指坐標的輪換對稱性,簡單的說就是將坐標軸重新命名,如果積分區間的函式表達不變,則被積函式中的x,y,z也同樣作變化後,積分值保持不變。...
二重積分是二元函式在空間上的積分,同定積分類似,是某種特定形式的和的極限。本質是求曲頂柱體體積。重積分有著廣泛的套用,可以用來計算曲面的面積,平面薄片重心等...
假定一個法向量在某個空間中的光滑曲面上的一條閉曲線移動,並保持它是曲面的法向量,如果不管如何選擇閉曲線,當回到出發點時法向量的指向與它原來的指向總是一致...
積分變換無論在數學理論或其套用中都是一種非常有用的工具。最重要的積分變換有傅立葉變換、拉普拉斯變換。由於不同套用的需要,還有其他一些積分變換,其中套用較為...
《微積分第三版下冊》是2001年高等教育出版社出版的圖書, 由同濟大學數學系編寫。本書主要介紹了向量代數與空間解析幾何,多元函式微分學,重積分,曲線積分與曲面積分...
《高等數學第Ⅲ卷多元微積分與微分幾何初步》是1997年清華大學出版社出版的圖書,作者是蕭樹鐵。...
本書補充了大量的數學工具,以此作為進一步研究微積分的起點,將大量的微積分概念有機地、 巧妙地結合起來處理數學命題,注重從命題本身的不同側面發現那些處理命題的不...
《考研微積分500例》是2009年國防工業出版社出版的圖書。...... 《考研微積分500例》是2009年國防工業出版社出版...16.曲線積分與曲面積分17.含參變數的積分...
它給出了閉曲面積分和相應體積分的積分變換關係,是矢量分析中的重要恆等式,也是研究場的重要公式之一。 物理套用 矢量分析 高斯定理是矢量分析的重要定理之一。...
雙層位勢(double layer potential)通過基本解的法嚮導數定義的一個曲面積分,也是拉普拉斯方程的一個特解。拉普拉斯方程以法國數學家、天文學家P.S.拉普拉斯(Pierre ...
斯托克斯公式是微積分基本公式在曲面積分情形下的推廣,它也是格林公式的推廣,這一公式給出了在曲面塊上的第二類曲面積分與其邊界曲線上的第二類曲線積分之間的聯繫。...
解答題之計算題應對策略:計算題考查重點不在於計算量和運算複雜度,而側重於思路和方法,例如重積分、曲線曲面積分的計算、求級數的和函式等,除了保證運算的準確率,...
曲面法向量在定義向量場的曲面積分中有著重要套用。[1] 在三維計算機圖形學中通常使用曲面法線進行光照計算。[2] 參考資料 [1] 吳傳生. 經濟數學——微積分 (第...
對極小立體角做曲面積分即可得立體角:立體角任意定向曲面 任意定向曲面相對於某一個點 P 的立體角,即為該曲面投影到以 P為球心的單位球面上的面積。 令 為該...
第十章 曲線積分與曲面積分239一、知識要點239二、方法歸納240三、題型攻略242題型1 對弧長的曲線積分計算242題型2 對坐標的曲線積分計算243...
涉及內容有函式與極限,單變數函式的微分學,不定積分,定積分、級數,多變數函式的微分學,帶參變數積分以及重積分與曲線積分、曲面積分等等,概括了數學分析的全部主題...
曲面法線在定義向量場的曲面積分中有著重要套用。 在三維計算機圖形學中通常使用曲面法線進行光照計算;參見朗伯餘弦定律(Lambert's cosine law)。...
積分表、習題答案與提示 [2] ;下冊包括空間解析幾何與向量代數、多元函式微分法及其套用、重積分、曲線積分與曲面積分、無窮級數等內容,書末還附有習題答案與提示 ...
在電磁學中,電通量(符號:ΦE)是電場的通量,與穿過一個曲面的電場線的數目成正比,是表征電場分布情況的物理量。...
