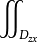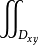第二型曲面積分是關於在坐標面投影的曲面積分，其物理背景是流量的計算問題。第二型曲線積分與積分路徑有關，第二型曲面積分同樣依賴於曲面的取向，第二型曲面積分與曲面的側有關，如果改變曲面的側(即法向量從指向某一側改變為指另一側)，顯然曲面積分要改變符號，注意在上述記號中未指明哪側，必須另外指出，第二型曲面積分有類似於第二型曲線積分的一些性質。
基本介紹
- 中文名：第二型曲面積分
- 所屬學科：數學（微積分）
- 簡介：關於在坐標面投影的曲面積分
- 物理背景：流量的計算問題
物理意義,第二型曲面積分的計算,
物理意義
第二型曲面積分的物理背景是流量的計算問題。設某流體的流速為v=((P(x，y，z)，Q(x，y，z)，R(x，y，z))從某雙側曲面S的一側流向另一側，求單位時間內流經該曲面的流量。由於是有向曲面，設它的單位法向量為n=(coα，cosβ，cosγ)，取曲面面積微元dS，則所求的單位時間內流量微元就是dE=(v·n)dS，若記有向曲面向量微元為dS=ndS，則dE=v·dS，那么，所求的通過整個曲面S的流量為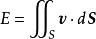
，若記
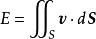
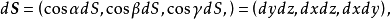
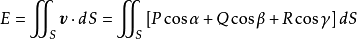
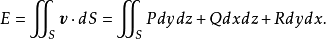
這種類型的積分稱為第二型曲面積分。P(x，y，z)稱為被積函式，S稱為積分曲面。
第二型曲面積分的計算
轉化為二重積分，必須注意兩個問題：
(1)將曲面S向相應的坐標平面投影，求得二重積分的積分區域。
(2)根據曲面的側（即法向量的方向）確定二重積分的符號。
根據積分表達式，確定投影平面，如要計算
P(x，y，z)dydz，必須將S向yz平面投影，求
得二重積分的積分區域Dyz，此時P(x，y，z)dydz=±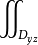
P(x(y，z)，y，z)dydz，其中曲面S：x=x(y，z)，(y，z)∈Dyz，二重積分的符號取決於法向量與x正向的夾角，為銳角時取正號，鈍角時取負號，簡記為前正、後負。
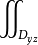
同理
