基本介紹
- 中文名:二重積分
- 外文名:double integral
- 性質:數學術語
- 計算方法:化為二次積分
- 本質:曲頂柱體體積
- 套用學科:數學
定義,性質,意義,幾何意義,數值意義,直角坐標系中,X型區域,Y型區域,在極坐標中,
定義
設二元函式z=f(x,y)定義在有界閉區域D上,將區域D任意分成n個子域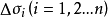 ,並以
,並以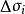 表示第
表示第 個子域的面積。在
個子域的面積。在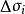 上任取一點
上任取一點 作和
作和 。如果當各個子域的直徑中的最大值
。如果當各個子域的直徑中的最大值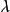 趨於零時,此和式的極限存在,且該極限值與區域D的分法及
趨於零時,此和式的極限存在,且該極限值與區域D的分法及 的取法無關,則稱此極限為函式
的取法無關,則稱此極限為函式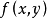 在區域
在區域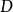 上的二重積分,記為
上的二重積分,記為 ,即
,即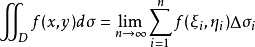 。
。
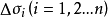
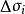

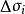


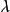

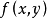
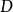

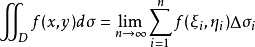
這時,稱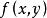 在
在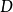 上可積,其中
上可積,其中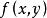 稱被積函式,
稱被積函式, 稱為被積表達式,
稱為被積表達式,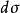 稱為面積元素,
稱為面積元素, 稱為積分區域,
稱為積分區域,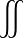 稱為二重積分號。
稱為二重積分號。
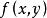
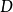
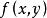

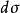

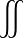
同時二重積分有著廣泛的套用,可以用來計算曲面的面積,平面薄片重心,平面薄片轉動慣量,平面薄片對質點的引力等等。此外二重積分在實際生活,比如無線電中也被廣泛套用。
性質
積分的線性性質
性質1 (積分可加性) 函式和(差)的二重積分等於各函式二重積分的和(差),即

性質2 (積分滿足數乘) 被積函式的常係數因子可以提到積分號外,即

比較性
性質3 如果在區域D上有f(x,y)≦g(x,y),則

估值性
性質4 設M和m分別是函式f(x,y)在有界閉區域D上的最大值和最小值,σ為區域D的面積,
則

性質5 如果在有界閉區域D上f(x,y)=k(k為常數),σ為D的面積,則Sσ=k∫∫dσ=kσ。
二重積分中值定理
設函式f(x,y)在有界閉區域D上連續,σ為區域的面積,則在D上至少存在一點(ξ,η),使得

意義
當被積函式大於零時,二重積分是柱體的體積。
當被積函式小於零時,二重積分是柱體體積負值。
幾何意義
在空間直角坐標系中,二重積分是各部分區域上柱體體積的代數和,在xoy平面上方的取正,在xoy平面下方的取負。某些特殊的被積函式f(x,y)的所表示的曲面和D底面所為圍的曲頂柱體的體積公式已知,可以用二重積分的幾何意義的來計算。
例如二重積分 ,其中
,其中 ,表示的是以上半球面為頂,半徑為a的圓為底面的一個曲頂柱體,這個二重積分即為半球體的體積
,表示的是以上半球面為頂,半徑為a的圓為底面的一個曲頂柱體,這個二重積分即為半球體的體積 。
。



數值意義
二重積分和定積分一樣不是函式,而是一個數值。因此若一個連續函式f(x,y)內含有二重積分,對它進行二次積分,這個二重積分的具體數值便可以求解出來。
如函式 ,其積分區域D是由
,其積分區域D是由 所圍成的區域。
所圍成的區域。


其中二重積分是一個常數,不妨設它為A。對等式兩端對D這個積分區域作二重定積分。



故這個函式的具體表達式為:f(x,y)=xy+1/8,等式的右邊就是二重積分數值為A,而等式最左邊根據性質5,可化為常數A乘上積分區域的面積1/3,將含有二重積分的等式可化為未知數A來求解。
直角坐標系中
當f(x,y)在區域D上可積時,其積分值與分割方法無關,可選用平行於坐標軸的兩組直線來分割D,這時每個小區域的面積Δσ=Δx·Δy,因此在直角坐標系下,面積元素dσ=dxdy,從而二重積分可以表示為
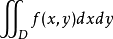
由此可以看出二重積分的值是被積函式和積分區域共同確定的。將上述二重積分化成兩次定積分的計算,稱之為:化二重積分為二次積分或累次積分。
X型區域
設積分區域是由兩條直線x=a,x=b(a<b),兩條曲線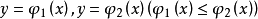 圍成。可以表示
圍成。可以表示 的區域稱為X型區域,如圖。
的區域稱為X型區域,如圖。 X型區域
X型區域
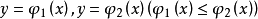

 X型區域
X型區域特點:穿過D內部且平行於y軸的直線,與D的邊界交點數不多於兩點。
如左圖,對任意取定的x0∈[a,b],過點(x0,0,0)作垂直於x軸的平面x=x0,該平面與曲頂柱體相交所得截面是以區間 為底,z=f(x0,y)為曲邊的曲邊梯形,由於x0的任意性,這一截面的面積為
為底,z=f(x0,y)為曲邊的曲邊梯形,由於x0的任意性,這一截面的面積為 ,其中y是積分變數在積分過程中視x為常數。上述曲頂柱體可看成平行截面面積S(x)從a到b求定積分的體積,從而得到:
,其中y是積分變數在積分過程中視x為常數。上述曲頂柱體可看成平行截面面積S(x)從a到b求定積分的體積,從而得到: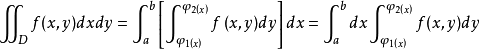


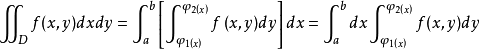
Y型區域
積分區域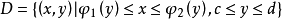 稱為Y型區域。
稱為Y型區域。 Y型區域
Y型區域
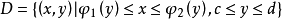
 Y型區域
Y型區域特點:穿過D內部且平行於x軸的直線,與D的邊界交點數不多於兩點。
稱D為Y型區域,此時可採用先對x,後對y積分的積分次序,將二重定積分化為累次積分:

在極坐標中
在直角坐標系xOy中,取原點為極坐標的極點,取正x軸為極軸,則點P的直角坐標系(x,y)與極坐標軸(r,θ)之間有關係式:


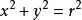

在極坐標系下計算二重積分,需將被積函式f(x,y),積分區域D以及面積元素dσ都用極坐標表示。函式f(x,y)的極坐標形式為f(rcosθ,rsinθ)。為得到極坐標下的面積元素dσ的轉換,用坐標曲線網去分割D,即用以r=a,即O為圓心r為半徑的圓和以θ=b,O為起點的射線去無窮分割D,設Δσ就是r到r+dr和從θ到θ+dθ的小區域,其面積為 ,可得到二重積分在極坐標下的表達式:
,可得到二重積分在極坐標下的表達式:




