基本介紹
- 中文名:極坐標系
- 外文名:Polar Coordinate System
- 創始人:牛頓
- 屬於:流數法與無窮級數
- 類型:二維坐標系統
- 套用學科:數學
歷史
射影




轉換






來源
極坐標系
 點(3,60°) 和 點(4,210°)
點(3,60°) 和 點(4,210°)


極坐標方程
 方程為r(θ)=1的圓
方程為r(θ)=1的圓 方程為 r(θ) = 2 sin 4θ的玫瑰線
方程為 r(θ) = 2 sin 4θ的玫瑰線 一條阿基米德螺線
一條阿基米德螺線

套用
計算二重積分
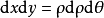












 點(3,60°) 和 點(4,210°)
點(3,60°) 和 點(4,210°)


 方程為r(θ)=1的圓
方程為r(θ)=1的圓 方程為 r(θ) = 2 sin 4θ的玫瑰線
方程為 r(θ) = 2 sin 4θ的玫瑰線 一條阿基米德螺線
一條阿基米德螺線

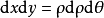

極坐標,屬於二維坐標系統,創始人是牛頓,主要套用於數學領域。在平面內取一個定點O,叫極點,引一條射線Ox,叫做極軸,再選定一個長度單位和角度的正方向(通常取逆...
極坐標系(polar coordinates)是指在平面內由極點、極軸和極徑組成的坐標系。在平面上取定一點O,稱為極點。從O出發引一條射線Ox,稱為極軸。再取定一個單位長度...
極坐標法是在控制點上測設一個角度和一段距離來確定點的平面位置。...... 用極坐標系描述的曲線方程稱作極坐標方程,通常表示為r為自變數θ的函式。...
在數學中,極坐標系是一個二維坐標系統。該坐標系統中任意位置可由一個夾角和一段相對原點—極點的距離來表示。極坐標系的套用領域十分廣泛,包括數學、物理、工程、...
平面極坐標是指在平面內取一個定點O, 叫極點,引一條射線Ox,叫做極軸,再選定一個長度單位和角度的正方向(通常取逆時針方向)。對於平面內任何一點M,用r表示線段...
《極坐標圖》是一款IOS平台的套用,是一個免費的評估版本iRegatta。 所有的功能都包括在內,但GPS和NMEA輸入後4分鐘內將關閉。可以買到所有你想使用的功能,如在...
極坐標定位(polar coordinate positioning)又稱方位—距離定位,是通過測定待定點到至少一個已知點的距離和方位所進行的一種無線電定位。...
平面極坐標系坐標系的一種。極坐標系在平面內由極點、極軸和極徑組成的坐標系。在平面上取一定點o,稱為極點,由o出發的一條射線ox,稱為極軸。對於平面上任意一...
球極坐標系,又稱空間極坐標,是三維坐標系的一種,由二維極坐標系擴展而來,用以確定三維空間中點、線、面以及體的位置,它以坐標原點為參考點,由方位角、仰角和...
用極坐標系所進行的測量方法稱做極坐標測量法。...... ,ρ叫做點M的極徑,θ叫做點M的極角,有序數對 (ρ,θ)就叫點M的極坐標,這樣建立的坐標系叫做極坐標...
極坐標定積分是以R為半徑,θ為積分變元,計算曲線周長的、面積的積分。曲線的周長定積分為,曲線的面積定積分為。設曲線ρ=R在區間[θ1,θ2]上非負連續,當d...
極坐標模式是由V.French等(1976)為了說明新建再生(epi-morphosis,參見再生)的調節機理而提出的。...
是平面坐標系的一種。通過到兩個固定點的距離來確定點的位置。...... 平面雙極坐標系是平面坐標系的一種,它以兩個定點O1,O2為極點(原點),並以定長為長度單...
所謂極坐標插補,是指車銑複合數控工具機本身具有1個旋轉軸和1個移動軸,旋轉軸實現極坐標下的極角改變,移動軸實現極徑改變,兩軸在位置控制模式下實現旋轉與移動聯動...
拋物線的極坐標方程是以焦點F(p/2,0)為圓心,R為變半徑的曲線方程...... (準線)距離相等的點的軌跡,拋物線的極坐標方程是拋物線以焦點為圓心,R為變半徑的曲線...
絕對極坐標:是指通過輸入某點距當前坐標原點的距離,及在該坐標平面中該點與坐標原點連線與x軸正向夾角來確定點的位置。 ...
Ρ ρ rho /rou/ 電阻係數,柱坐標和極坐標中的極徑,密度 ∑ σ ς sigma /'sigmə/ 總和,表面密度,跨導,正應力 Τ τ tau /tau/ 時間常數,切應...
對於平面內任何一點M,用ρ表示線段OM的長度,θ表示從Ox到OM的角度,ρ叫做點M的極徑,θ叫做點M的極角,有序數對(ρ,θ)就叫點M的極坐標,這樣建立的坐標系...
它的極坐標方程為:r = aθ這種螺線的每條臂的距離永遠相等於 2πa。笛卡爾坐標方程式為:r=10*(1+t)x=r*cos(t * 360)y=r*sin(t * 360)...
1、在圓錐中,圓錐曲線極坐標方程可表示為:其中l表示半徑,e表示離心率;2、在平面坐標系中,圓錐曲線極坐標方程可表示為:其中e表示離心率,p表示焦點到準線的距離。...
