基本介紹
- 中文名：平面直角坐標系
- 外文名：Plane Rectangular Coordinate System
- 簡稱：直角坐標系
- 創立者：勒內·笛卡爾
- 套用學科：數學
- 套用領域：函式
發展歷程,坐標系,點的坐標,象限,對稱點,點的符號,性質,高斯平面直角坐標系,投影方法,特點,套用,
發展歷程
坐標的思想是法國數學家、哲學家笛卡爾所創立的。
笛卡爾
笛卡爾傳說：
有一天，笛卡爾（Descartes 1596—1650，法國哲學家、數學家、物理學家）生病臥床，但他頭腦一直沒有休息，在反覆思考一個問題：幾何圖形是直觀的，而代數方程則比較抽象，能不能用幾何圖形來表示方程呢？這裡，關鍵是如何把組成幾何的圖形的點和滿足方程的每一組“數”掛上鉤。他就拚命琢磨。通過什麼樣的辦法、才能把“點”和“數”聯繫起來。突然，他看見屋頂角上的一隻蜘蛛，拉著絲垂了下來，一會兒，蜘蛛又順著絲爬上去，在上邊左右拉絲。蜘蛛的“表演”，使笛卡爾思路豁然開朗。他想，可以把蜘蛛看做一個點，它在屋子裡可以上、下、左、右運動，能不能把蜘蛛的每個位置用一組數確定下來呢？他又想，屋子裡相鄰的兩面牆與地面交出了三條直線，如果把地面上的牆角作為起點，把交出來的三條線作為三根數軸，那么空間中任意一點的位置，不是都可以用這三根數軸上找到的有順序的三個數來表示嗎？反過來，任意給一組三個有順序的數，例如3、2、1，也可以用空間中的一個點 P來表示它們。同樣，用一組數（a， b）可以表示平面上的一個點，平面上的一個點也可以用一組二個有順序的數來表示。於是在蜘蛛的啟示下，笛卡爾創建了直角坐標系。
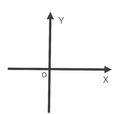
坐標系
在平面“二維”內畫兩條互相垂直，並且有公共原點的數軸，簡稱直角坐標系。平面直角坐標系有兩個坐標軸，其中橫軸為x軸(x-axis)，取向右方向為正方向；縱軸為y軸（y-axis)，取向上為正方向。坐標系所在平面叫做坐標平面，兩坐標軸的公共原點叫做平面直角坐標系的原點。x軸y軸將坐標平面分成了四個象限（quadrant），右上方的部分叫做第一象限，其他三個部分按逆時針方向依次叫做第二象限、第三象限和第四象限。象限以數軸為界，橫軸、縱軸上的點及原點不在任何一個象限內。一般情況下，x軸y軸取相同的單位長度，但在特殊的情況下，也可以取不同的單位長度。
點的坐標
在直角坐標系中，對於平面上的任意一點，都有唯一的一個有序數對（即點的坐標(coordinates)）與它對應；反過來，對於任意一個有序數對，都有平面上唯一的一點與它對應。
對於平面內任意一點C，過點C分別向x軸、y軸作垂線，垂足在x軸、y軸上的對應點a,b分別叫做點C的橫坐標、縱坐標，有序數對(ordered pair)（a,b）叫做點C的坐標。一個點在不同的象限或坐標軸上，點的坐標不一樣。
特殊位置的點的坐標的特點：
1.x軸上的點的縱坐標為零；y軸上的點的橫坐標為零。
2.在任意的兩點中，如果兩點的橫坐標相同，則兩點的連線平行於縱軸（兩點的橫坐標不為零）；如果兩點的縱坐標相同，則兩點的連線平行於橫軸（兩點的縱坐標不為零）。
3.點到軸及原點的距離：
點到x軸的距離為|y|； 點到y軸的距離為|x|；點到原點的距離為x的平方加y的平方的算術平方根。
象限
對稱點
1.關於x軸成軸對稱的點的坐標，橫坐標相同，縱坐標互為相反數。（橫同縱反）
2.關於y軸成軸對稱的點的坐標，縱坐標相同，橫坐標互為相反數。（橫反縱同）
3.關於原點成中心對稱的點的坐標，橫坐標與橫坐標互為相反數，縱坐標與縱坐標互為相反數。（橫縱皆反）
點的符號
橫坐標 縱坐標
第一象限：（+，+）正正
第二象限：（-，+）負正
第三象限：（-，-）負負
第四象限：（+, -）正負
x軸正半軸：（+，0）
x軸負半軸：（-，0）
y軸正半軸：（0，+)
y軸負半軸： (0，-）
x軸上的點的縱坐標為0，y軸上的點的橫坐標為0。
原點：（0，0）
註：以數對形式（x，y）表示的坐標系中的點。如（2，-4），“2”是x軸坐標，“-4”是y軸坐標。
1.第一象限中的點的橫坐標(x)大於0，縱坐標(y)大於0。
2.第二象限中的點的橫坐標(x)小於0，縱坐標(y)大於0。
3.第三象限中的點的橫坐標(x)小於0，縱坐標(y)小於0。
4.第四象限中的點的橫坐標(x)大於0，縱坐標(y)小於0。
各象限角平分線的點的特徵：
一、三象限角平分線上的點p (a,b）橫縱坐標相等，即a=b；
二、四象限角平分線上的點p (a,b)橫縱坐標相反，即a+b=0或a=-b。
性質
1.坐標平面內的點與有序實數對一一對應。
2. 一三象限角平分線上的點橫縱坐標相等。
3.二四象限角平分線上的點橫縱坐標互為相反數。
4.一點上下平移，橫坐標不變，即平行於y軸的直線上的點橫坐標相同。
5.y軸上的點，橫坐標都為0。
6.x軸上的點，縱坐標都為0。
7.坐標軸上的點不屬於任何象限。
8.一個關於x軸對稱的點橫坐標不變，縱坐標變為原坐標的相反數。反之同樣成立。
9.一個關於原點對稱的點橫縱坐標均為原坐標相反數。
10.與x軸做軸對稱變換時，x不變，y變為相反數。
11.與y軸做軸對稱變換時，y不變，x變為相反數。
12.與原點做軸對稱變換時，y與x都變為相反數。
高斯平面直角坐標系
投影方法
高斯投影的方法是將地球按經線劃分為帶，稱為投影帶。投影是從首子午線開始的，分6°帶和3°兩種。每隔6°劃分一帶的叫6°帶，每隔3°劃分一帶的叫3°帶。我國領土位於東經72°∽136°之間，共包括了11個6°帶，即13∽23帶；22個3°投影帶即24∽45帶。
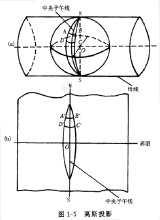
構想一個平面捲成橫圓柱套在地球外，如圖1－5（a)所示 。通過高斯投影，將中央子午線的投影作為
縱坐標軸，用x表示，將赤道的投影作橫坐標軸，用y表示，兩軸的交點作為坐標原點，由此構成的平面直角坐標系稱為高斯平面直角坐標系，如圖1－5（b) 所示。每一個投影帶都有一個獨立的高斯平面直角坐標系，區分各帶坐標系則利用相應投影帶的帶號。在每一個投影帶內，y坐標值都有正有負，這對於計算和使用都不方便，為了使y坐標都為正值，故將縱坐標軸向西平移500㎞，並在y坐標前加上投影帶的帶號。 6°帶投影是從英國格林尼治子午線開始，自西向東，每隔經差6°分為一帶，將地球分為60個帶，其編號分別為1，2，3，…60。任意帶的中央子午線經度為Lo，它與投影帶號N的關係如下所示：
Lo=(6N-3°)
式中：N———6°帶的帶號
離中央子午線越遠，長度變形越大，在要求較小的投影變形時，可採用3°投影帶。3°帶是在6°帶的基礎上劃分的，如圖所示。每3°為一帶，從東經1°30′開始，共120帶，其中央子午線在奇數帶時與6°帶的中央子午線重合，每帶的中央子午線可用下面的工式計算：
Lo=3N′
式中：N′——3°帶的帶號。
為了避免y坐標出現負值，3°帶的坐標原點同6°帶一樣，向西移動500㎞，並在y坐標前加3°帶的帶號。
特點
應當注意的是，高斯投影沒有角度變形，但有長度變形和面積變形，離中央子午線越遠，變形就越大。其主要特點有以下三點：
（1）投影后中央子午線為直線，長度不變形，其餘經線投影對稱並且凹向於中央子午線，離中央子午線越遠，變形越大。
（2）赤道的投影也為一直線，並與中央子午線正交，其餘的經緯投影為凸向赤道的對稱曲線。
（3）經緯投影后仍然保持相互垂直的關係，投影后有角度無變形。
套用
用直角坐標原理在投影面上確定地麵點平面位置的坐標系：
與數學上的直角坐標系不同的是，它的橫軸為Y軸，縱軸為X軸。在投影面上，由投影帶中央經線的投影為調軸、赤道投影為橫軸（Y軸）以及它們的交點為原點的直角坐標系稱為國家坐標系，國家坐標系（national coordinate system）是各國為進行測繪和處理其成果，規定在全國範圍內使用統一坐標框架的坐標系統,又稱國家大地坐標系。國家大地坐標系是測制國家基本比例尺地圖的基礎。否則稱為獨立坐標系。
坐標方法的簡單套用：
1.用坐標表示地理位置。
2.用坐標表示平移。
在測量學中使用的平面直角坐標系統（rectangular plane coordinate system）包括高斯平面直角坐標系和獨立平面直角坐標系。
