基本介紹
- 中文名:坐標
- 外文名:coordinate
- 基本要素:基本平面,主點
- 作用:確定位置
- 種類:相對,絕對,相對極坐標
- 領域:數學
分類
簡介
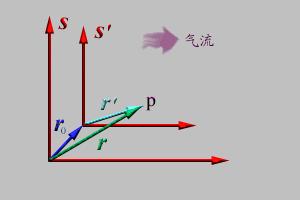 氣流的坐標
氣流的坐標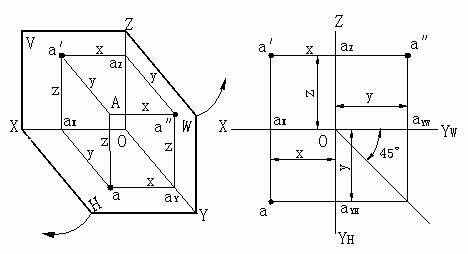 坐標
坐標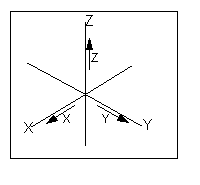 笛卡爾坐標系
笛卡爾坐標系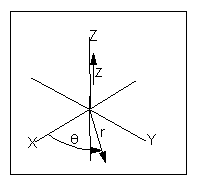 柱坐標系
柱坐標系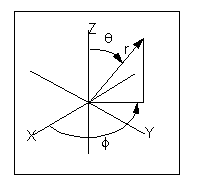 球坐標系
球坐標系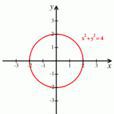
 氣流的坐標
氣流的坐標 坐標
坐標 笛卡爾坐標系
笛卡爾坐標系 柱坐標系
柱坐標系 球坐標系
球坐標系為確定天球上某一點的位置,在天球上建立的球面坐標系。有兩個基本要素:①基本平面。由天球上某一選定的大圓所確定。大圓稱為基圈,基圈的兩個幾何極之一,...
為了說明質點的位置、運動的快慢、方向等,必須選取其坐標系。在參照系中,為確定空間一點的位置,按規定方法選取的有次序的一組數據,這就叫做“坐標”。在某一...
點坐標(coordinate of point)空間點位置的表示,以三個投影面作為坐標面,三個投影軸作為坐標軸,則空間點B到投影面的有向線段,稱為點的坐標。...
坐標系統,是描述物質存在的空間位置(坐標)的參照系,通過定義特定基準及其參數形式來實現。坐標是描述位置的一組數值,按坐標的維度一般分為一維坐標(公路里程碑)和...
球坐標系是三維坐標系的一種,用以確定三維空間中點、線、面以及體的位置,它以坐標原點為參考點,由方位角、仰角和距離構成。球坐標系在地理學、天文學中都有著...
色坐標是色度學的重要內容之一,光源的色坐標測量是研究光源特性的重要方法之一,它具有廣泛的使用意義。色坐標測量的基本原理是根據光源的光譜分布由色坐標的基本規定...
地理坐標是用緯度、經度表示地麵點位置的球面坐標。地理坐標系以地軸為極軸,所有通過地球南北極的平面均稱為子午面。地理坐標,就是用經緯度表示地麵點位的球面坐標...
“曲線坐標”是天文學專有名詞。曲線坐標計算程式可計算圓曲線帶有緩和曲線、邊樁坐標及切線方位角,附有正算、反算功能。正算:通過里程和偏距計算坐標;反算:通過...
坐標(coordinates)是遊戲《minecraft》里用來確定方位的一種東西,通過數字的變化來反映玩家所在的位置。坐標基於一個由三條交於一點(即原點)的坐標軸而形成的格線。...
坐標軸(coordinate axis)用來定義一個坐標系的一組直線或一組線;位於坐標軸上的點的位置由一個坐標值所唯一確定,而其他的坐標軸上的點的位置由一個坐標值所唯一...
大地坐標系是大地測量中以參考橢球面為基準面建立起來的坐標系。地麵點的位置用大地經度、大地緯度和大地高度表示。大地坐標系的確立包括選擇一個橢球、對橢球進行...
數學中,重心坐標是由單形(如三角形或四面體等)頂點定義的坐標。重心坐標是齊次坐標的一種。...
國家坐標系(national coordinate system)是各國為進行測繪和處理其成果,規定在全國範圍內使用統一坐標框架的坐標系統,又稱國家大地坐標系。國家大地坐標系是測制國家...
北京54坐標系(BJZ54)是指北京54坐標係為參心大地坐標系,大地上的一點可用經度L54、緯度M54和大地高H54定位,它是以克拉索夫斯基橢球為基礎,經局部平差後產生的...
笛卡兒平面直角坐標系中平行於縱坐標軸的方向與某一方向的夾角。坐標方位角是平面直角坐標系中某一直線與坐標主軸(X軸)之間的夾角,從主軸起算,順時針方向自0~360...
坐標轉換是空間實體的位置描述,是從一種坐標系統變換到另一種坐標系統的過程。通過建立兩個坐標系統之間一一對應關係來實現。是各種比例尺地圖測量和編繪中建立地圖...
齊次坐標就是將一個原本是n維的向量用一個n+1維向量來表示,是指一個用於投影幾何里的坐標系統,如同用於歐氏幾何里的笛卡兒坐標一般。...
極坐標系(polar coordinates)是指在平面內由極點、極軸和極徑組成的坐標系。在平面上取定一點O,稱為極點。從O出發引一條射線Ox,稱為極軸。再取定一個單位長度...
時間坐標,“非常喜歡”的一家咖啡館,“人不多”,“安靜”、“溫暖”。桌椅沙發“幾乎沒有相同的”,感覺“每一個角落”都有一個屬於自己的“故事”。書架上...
在平面內畫兩條互相垂直,並且有公共原點的數軸。其中橫軸為X軸,縱軸為Y軸。這樣我們就說在平面上建立了平面直角坐標系,簡稱直角坐標系。還分為第一象限,第二...
直角坐標系又叫笛卡爾坐標系,它通過一對數字坐標在平面中唯一地指定每個點,該坐標系是以相同的長度單位測量的兩個固定的垂直有向線的點的有符號距離。每個參考線...
縱坐標(vertical ordinate),也稱y坐標,縱坐標與橫坐標構成笛卡爾坐標系(直角坐標系)以表示函式的圖像。...
三維坐標,是指通過相互獨立的三個變數構成的具有一定意義的點。它表示空間的點,在不同的三維坐標系下,具有不同的表達形式。...
世界坐標系是系統的絕對坐標系,在沒有建立用戶坐標系之前畫面上所有點的坐標都是以該坐標系的原點來確定各自的位置的。...
