基本介紹
- 中文名:重心坐標
- 外文名:barycentric coordinates
- 領域:數學
- 分類:在直線上與在平面上
- 定義:由單形頂點定義
- 相關坐標:內心坐標
定義
直線上的重心坐標



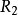









平面上的重心坐標

























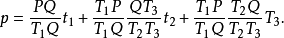



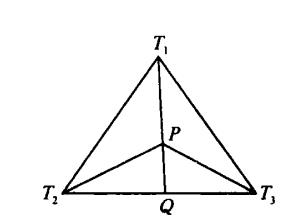 圖1
圖1與內心坐標的關係







































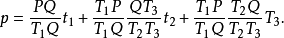



 圖1
圖1
數學中,重心坐標是由單形(如三角形或四面體等)頂點定義的坐標。重心坐標是齊次坐標的一種。...
船舶在重力場中,物體處於任何方位時所有各組成支點的重力的合力都通過的那一點成為船的重心。船舶重心至中線面的距離成為船重心橫向坐標。...
質點系重心坐標(coordinates of the barycen-ter of a particle system)是一種特殊坐標,它是確定質點系重心位置的計算公式。質點系中各質點的質量是定值時,質點...
重心,是在重力場中,物體處於任何方位時所有各組成支點的重力的合力都通過的那一點。規則而密度均勻物體的重心就是它的幾何中心。不規則物體的重心,可以用懸掛法來...
三角形重心是三角形三條中線的交點。當幾何體為勻質物體時,重心與形心重合。...... 顯然當x=(x1+x2+x3)/3,y=(y1+y2+y3)/3(重心坐標)時上式取得最小...
三角形的三條邊的中線交於一點。該點叫做三角形的重心。三中線交於一點可用燕尾定理證明,十分簡單
數學上的重心是指三角形的三條中線的交點,其證明定理有燕尾定理或塞瓦定理,套用定理有梅涅勞斯定理、塞瓦定理。...
人口重心又稱人口中心(mean pointer centre),為地區人口分布的綜合統計與表示方法之一。...
飛機重心定位的定義就是整個飛機的重心和機翼的相對位置,它以翼弦長度的百分數表示。有關飛行重心定位的定義和概念有很多,如中性重心、最前和最後容許重心、最前和...
中文名稱 極限重心垂向坐標曲線 英文名稱 curve of limiting positions of center of gravity 定義 在符合穩性規範要求的條件下,以各排水量為橫坐標,船舶重心至...
三角形的重心,外心,垂心,內心和旁心稱之為三角形的五心。三角形五心定理是指三角形重心定理,外心定理,垂心定理,內心定理,旁心定理的總稱
