三角形重心

三角形重心是三角形三條中線的交點。當幾何體為勻質物體時，重心與形心重合。

基本介紹

• 中文名：三角形重心
• 外文名：centroid
• 定義：三角形三條中線的交點
• 性質比例：重心到頂點與到對邊中點比為2：1
• 套用領域：幾何

重心定義

三角形重心是三角形三邊每一邊的三條中線的交點。當幾何體為勻質物體時，重心與該形中心重合。

性質證明

1、重心到頂點的距離與重心到對邊中點的距離之比為2：1。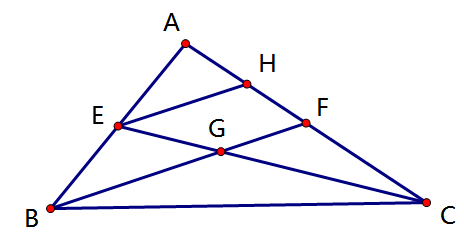

證明一

例：已知：△ABC，E、F是AB，AC的中點。EC、FB交於G。

求證：EG=1/2CG

證明：過E作EH∥BF交AC於H。

∵AE=BE，EH//BF

∴AH=HF=1/2AF(平行線分線段成比例定理)

又∵ AF=CF

∴HF=1/2CF

∴HF:CF=1/2

∵EH∥BF

∴EG:CG=HF:CF=1/2

∴EG=1/2CG

證明二

2、重心和三角形3個頂點組成的3個三角形面積相等。

證明方法：

在△ABC內，三邊為a，b，c，點O是該三角形的重心，AOA'、BOB'、COC'分別為a、b、c邊上的中線。根據重心性質知：

OA'=1/3AA'

OB'=1/3BB'

OC'=1/3CC'

過O，A分別作a邊上高OH'，AH

可知OH'=1/3AH

則，S_△BOC=1/2×OH'a=1/2×1/3AHa=1/3S_△ABC

同理可證S_△AOC=1/3S_△ABC

S_△AOB=1/3S_△ABC

所以，S_△BOC=S_△AOC=S_△AOB

3、重心到三角形3個頂點距離平方的和最小。 (等邊三角形）

證法一：

設三角形三個頂點為(x₁,y₁),(x₂,y₂),(x₃,y₃) 平面上任意一點為（x₀，y₀） 則該點到三頂點距離平方和為：

(x₁-x₀)²+(y₁-y₀)²+(x₂-x₀)²+(y₂-y₀)²+(x₃-x₀)²+(y₃-y₀)²

=3x₀²-2x₀(x₁+x₂+x₃)+3y₀²-2y₀(y₁+y₂+y₃)+x₁²+x₂²+x₃²+y₁²+y₂²+y₃²

=3[x₀-1/3*(x₁+x₂+x₃)]²+3[y₀-1/3*(y₁+y₂+y₃)]²+x₁²+x₂²+x₃²+y₁²+y₂²+y₃²-1/3(x₁+x₂+x₃)²-1/3(y₁+y₂+y₃)²

顯然當x=(x₁+x₂+x₃)/3,y=(y₁+y₂+y₃)/3（重心坐標）時

上式取得最小值x₁²+x₂²+x₃²+y₁²+y₂²+y₃²-1/3(x₁+x₂+x₃)²-1/3(y₁+y₂+y₃)²

最終得出結論。

證法二：由性質8（卡諾重心定理）可得出結論。

4、在平面直角坐標系中，重心的坐標是頂點坐標的算術平均數，

即其坐標為[(X₁+X₂+X₃)/3,(Y₁+Y₂+Y₃)/3]；

空間直角坐標系——X坐標：(X₁+X₂+X₃)/3，Y坐標：(Y₁+Y₂+Y₃)/3，Z坐標：（Z1+Z2+Z3）/3.

5、三角形內到三邊距離之積最大的點。

證明：如圖所示，點P是△ABC內的一點，連線PA，PB，PC，作點P到BC、AC、AB的垂線段，垂足分別為D、E、F，延長AP交BC於M。記△ABC的面積為S，BC為a，AC為b，AB為c，PD為a'，PE為b'，PF為c'。

∵aa'/2+bb'/2+cc'/2=S△BCP+S△ACP+S△ABP=S

∴aa'+bb'+cc'=2S

由均值不等式知，[(aa'+bb'+cc')/3]^3≥aa'bb'cc'=(abc)*(a'b'c')，若且唯若aa'=bb'=cc'時等號成立。

∴a'b'c'≤[(aa'+bb'+cc')/3]^3/(abc)=(S/3)^3/(abc)=8S^3/(27abc)，若且唯若aa'=bb'=cc'時等號成立。

∴a'b'c'只有當aa'=bb'=cc'時才會取得最大值。

此時，S△ABP=cc'/2=bb'/2=S△ACP，由燕尾定理知，BM/CM=S△ABP/S△ACP=1。

∴此時BM=CM，M是BC的中點，AM是△ABC的中線，P在△ABC中BC邊的中線上。

同理可證此時P在△ABC中AB、AC邊的中線上。

∴當a'b'c'最大時，P是△ABC的重心，即重心是三角形內到三邊距離之積最大的點。

6、在△ABC中，若MA向量+MB向量+MC向量=0（向量） ，則M點為△ABC的重心，反之也成立。

7、設△ABC重心為G點，所在平面有一點O，則向量OG=1/3（向量OA+向量OB+向量OC）

8、卡諾重心定理：若G為三角形ABC的重心,P為三角形ABC所在平面上任意一點，則PA^2+PB^2+PC^2=GA^2+GB^2+GC^2+3PG^2=1/3(a^2+b^2+c^2)+3PG^2

證明：GA^2 + PG^2 = PA^2 + 2GA*PGcos(AGP)
GB^2 + PG^2 = PB^2 + 2GB*PGcos(BGP)
GC^2 + PG^2 = PC^2 + 2GC*PGcos(CGP)
GA^2 + GB^2 + GC^2 + 3PG^2 = PA^2 + PB^2 + PC^2 + 2PG[GA*cos(AGP) + GB*cos(BGP) + GC*cos(CGP)]
延長射線AG,交BC於D,繼續延長,使得GD = DE = AG/2.
連線EB,EC,
四邊形GBEC為平行四邊形.
EB = GC
延長射線PG,
過點B作PG的延長線的垂線,垂足為F.
過點E作PG的延長線的垂線,垂足為H.
BE與PG的延長線的交點為點Q.
則,因GC//BE,角CGP = 角EQG = 角BQF
GH = GE*cos(EGH) = GA*cos(AGP)
HF = EB*cos(BQF) = GC*cos(EQG) = GC*cos(CGP)
而
GH + HF = GF = GB*cos(BGF) = GB*cos(PI-BGP) = -GB*cos(BGP),
因此,
GA*cos(AGP) + GB*cos(BGP) + GC*cos(CGP) = 0,
GA^2 + GB^2 + GC^2 + 3PG^2
= PA^2 + PB^2 + PC^2 + 2PG[GA*cos(AGP) + GB*cos(BGP) + GC*cos(CGP)]
= PA^2 + PB^2 + PC^2
利用上面的結論,
令P與A重合,有
GA^2 + GB^2 + GC^2 + 3GA^2
= AB^2 + AC^2 ...(1)
令P與B重合,有
GA^2 + GB^2 + GC^2 + 3GB^2
= AB^2 + BC^2 ...(2)
令P與C重合,有
GA^2 + GB^2 + GC^2 + 3GC^2
= BC^2 + AC^2 ...(3)
(1),(2),(3)相加,有
3[GA^2 + GB^2 + GC^2] + 3[GA^2 + GB^2 + GC^2] = 2[AB^2 + BC^2 + AC^2],
GA^2 + GB^2 + GC^2 = [AB^2 + BC^2 + AC^2]/3 = (a^2 + b^2 + c^2)/3.
得證.

順口溜

三條中線必相交，交點命名為重心

重心分割中線段，線段之比二比一；

向量關係

O是重心，向量OA+向量OB+向量OC=零向量。