三角形五心

三角形五心是指三角形的重心、外心、內心、垂心、旁心。三條中線的交點是重心，三邊垂直平分線的交點是外心，三條內角平分線的交點為內心，三角形三條高線的交點為垂心。

與三角形的一邊及其他兩邊的延長線都相切的圓叫做三角形的旁切圓，旁切圓的圓心叫做三角形旁心。

基本介紹

• 中文名：三角形五心
• 外文名：Five triangle
• 包含：重心 外心 內心 垂心 旁心
• 用途：數學

重心

重心

定理：設三角形重心為O，BC邊中點為D，則有AO = 2 OD。重心坐標為三頂點坐標平均值（在平面直角坐標系中，重心的坐標是頂點坐標的算術平均數，即其坐標為[(X1+X2+X3)/3,(Y1+Y2+Y3)/3]）。三條中線相交的點叫做重心。

外心

三角形三邊的垂直平分線的交點，稱為三角形外心。

外心

外心到三頂點距離相等。

過三角形各頂點的圓叫做三角形的外接圓，外接圓的圓心即三角形外心，這個三角形叫做這個圓的內接三角形。

三角形有且只有一個外接圓。

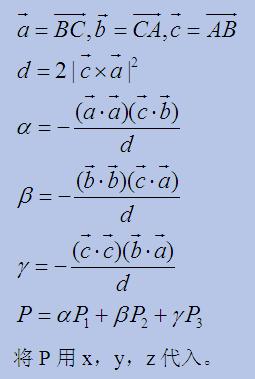外心公式：

外心公式

內心

三角形內心為三角形三條內角平分線的交點。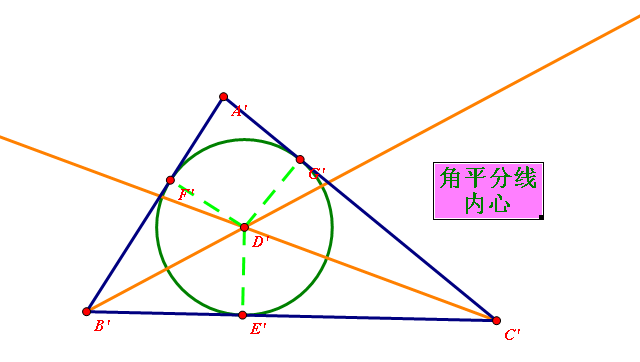

內心

與三角形各邊都相切的圓叫做三角形的內切圓，內切圓的圓心即是三角形內心，內心到三角形三邊距離相等。這個三角形叫做圓的外切三角形。

三角形有且只有一個內切圓。

內心坐標公式：

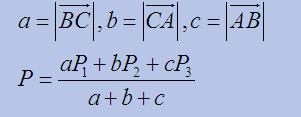內心坐標公式

垂心

三角形三邊上的三條高或其延長線交於一點，稱為三角形垂心。

垂心

銳角三角形的垂心在三角形內；直角三角形的垂心在直角的頂點；鈍角三角形的垂心在三角形外.。

三角形只有一個垂心。

垂心坐標公式：

垂心坐標公式

旁心

與三角形的一邊及其他兩邊的延長線都相切的圓叫做三角形的旁切圓，旁切圓的圓心叫做三角形旁心。

旁心

三角形的一條內角平分線與其他兩個角的外角平分線交於一點，即三角形的旁心。旁心到三角形一邊及其他兩邊延長線的距離相等。

三角形有三個旁切圓，三個旁心。這三個旁心到三角形三條邊的延長線的距離相等。

五心的性質

三角形的五心有許多重要性質，它們之間也有很密切的聯繫，如：

（1）三角形的重心與三頂點的連線所構成的三個三角形面積相等；

（2）三角形的外心到三頂點的距離相等；

（3）三角形的垂心與三頂點這四點中，任一點是其餘三點所構成的三角形的垂心；

（4）三角形的內心、旁心到三邊距離相等；

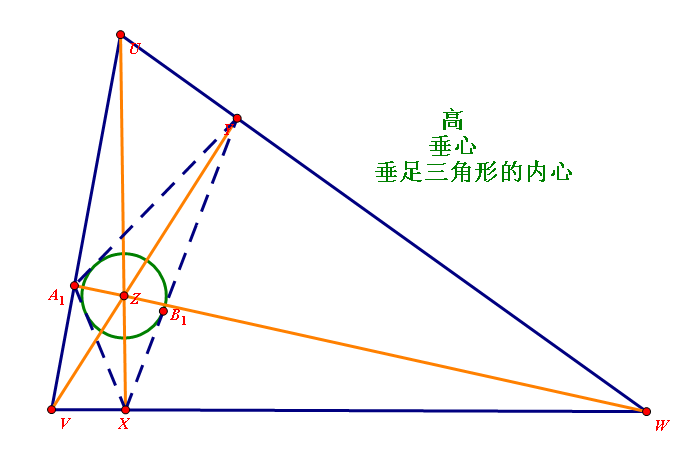
（5）三角形的垂心是它垂足三角形的內心；或者說，三角形的內心是它旁心三角形的垂心；

（6）三角形的外心是它的中點三角形的垂心；

（7）三角形的重心也是它的中點三角形的重心；

（8）三角形的中點三角形的外心也是其垂足三角形的外心．

（9）三角形的任一頂點到垂心的距離，等於外心到對邊的距離的二倍.

下面是更為詳細的性質：

垂心性質

三角形三邊上的高的交點稱為三角形的垂心。三角形垂心有下列有趣的性質：設△ABC的三條高為AD、BE、CF，其中D、E、F為垂足,垂心為H。

性質1垂心H關於三邊的對稱點，均在△ABC的外接圓上。

性質2 △ABC中,有六組四點共圓，有三組(每組四個)相似的直角三角形，且AH·HD=BH·HE=CH·HF。

性質3 H、A、B、C四點中任一點是其餘三點為頂點的三角形的垂心(並稱這樣的四點為一垂心組)。

性質4 △ABC,△ABH,△BCH,△ACH的外接圓是等圓。

性質5 在非直角三角形中,過H的直線交AB、AC所在直線分別於P、Q，則 AB/AP·tanB+ AC/AQ·tanC=tanA+tanB+tanC。

性質6 三角形任一頂點到垂心的距離，等於外心到對邊的距離的2倍。

性質7 設O，H分別為△ABC的外心和垂心，則∠BAO=∠HAC，∠ABH=∠OBC，∠BCO=∠HCA。

性質8銳角三角形的垂心到三頂點的距離之和等於其內切圓與外接圓半徑之和的2倍。

性質9銳角三角形的垂心是垂足三角形的內心；銳角三角形的內接三角形(頂點在原三角形的邊上)中，以垂足三角形的周長最短。

內心性質

三角形的內切圓的圓心簡稱為三角形的內心，即三角形三個角平分線的交點。內心有下列優美的性質：

性質1 設I為△ABC的內一點,則I為其內心的必要不充分條件是：到△ABC三邊的距離相等。

性質2 設I為△ABC的內心，則∠BIC=90°+1/2∠A，類似地還有兩式；反之亦然。

性質3 設I為△ABC內一點，AI所在直線交△ABC的外接圓於D。I為△ABC內心的充要條件是ID=DB=DC。

性質4 設I為△ABC的內心，BC=a，AC=b，AB=c，I在BC、AC、AB上的射影分別為D、E、F；內切圓半徑為r，令p= (a+b+c)，則(1)S△ABC=pr；(2)r=2S△ABC/a+b+c ；(3)AE=AF=p-a,BD=BF=p-b,CE=CD=p-c；(4)abcr=p·AI·BI·CI。

性質5 三角形一內角平分線與其外接圓的交點到另兩頂點的距離與到內心的距離相等；反之，若I為△ABC的∠A平分線AD(D在△ABC的外接圓上)上的點，且DI=DB，則I為△ABC的內心。

性質6 設I為△ABC的內心，BC=a，AC=b，AB=c，∠A的平分線交BC於K,交△ABC的外接圓於D，則 = = = 。

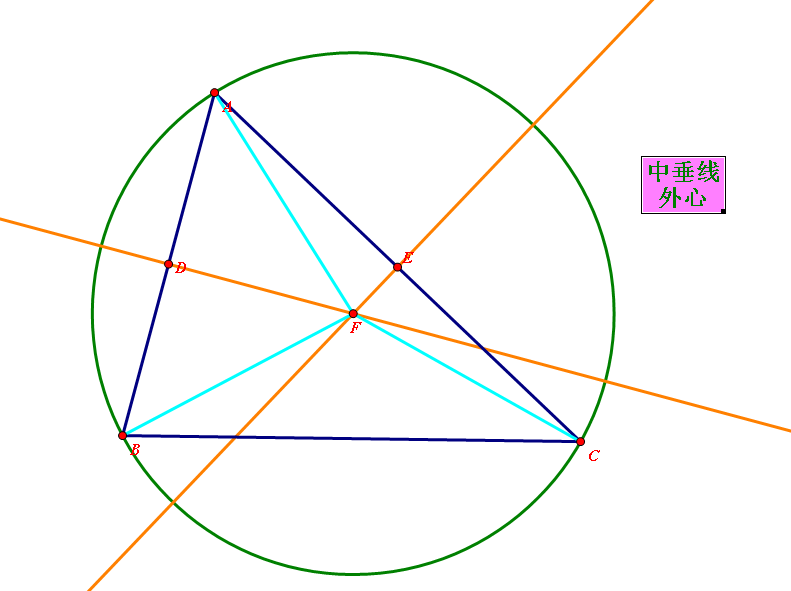
外心性質

三角形的外接圓的圓心簡稱三角形的外心.即三角形三邊中垂線的交點。外心有如下一系列優美性質：

性質1三角形的外心到三頂點的距離相等，反之亦然。

性質2 設O為△ABC的外心，則∠BOC=2∠A，或∠BOC=360°-2∠A(還有兩式)。

性質3 設三角形的三條邊長，外接圓的半徑、面積分別為a、b、c,R、S△，則R=abc/4S△。

性質4 過△ABC的外心O任作一直線與邊AB、AC(或延長線)分別相交於P、Q兩點，則AB/AP ·sin2B+ AC/AQ·sin2C=sin2A+sin2B+sin2C。

性質5銳角三角形的外心到三邊的距離之和等於其內切圓與外接圓半徑之和。

重心性質

性質1 設G為△ABC的重心，△ABC內的點Q在邊BC、CA、AB邊上的射影分別為D、E、F，則當Q與G重合時QD·QE·QF最大。

性質2 設G為△ABC的重心，AG、BG、CG的延長線交△ABC的三邊於D、E、F,則S_△AGF=S_△BGD=S_△CGE。

性質3 設G為△ABC的重心，則S_△ABG=S_△BCG=S_△ACG= S_△ABC。

旁心性質

1、三角形一內角平分線和另外兩頂點處的外角平分線交於一點，該點即為三角形的旁心。

2、每個三角形都有三個旁心。

3、旁心到三邊的距離相等。

記憶方法

三角形有五顆心，重外垂內和旁心， 五心性質很重要，認真掌握莫記混．

重心記憶口訣

三條中線定相交，交點位置真奇巧， 交點命名為“重心”，重心性質要明了，

重心分割中線段，數段之比聽分曉； 長短之比二比一，靈活運用掌握好．

外心記憶口訣

三角形有六元素，三個內角有三邊． 作三邊的中垂線，三線相交共一點．

此點定義為外心，用它可作外接圓． 內心外心莫記混，內切外接是關鍵．

垂心記憶口訣

角形上作三高，三高必於垂心交． 高線分割三角形，出現直角三對整，

直角三角形有十二，構成六對相似形， 四點共圓圖中有，細心分析可找清.

內心記憶口訣

三角對應三頂點，角角都有平分線， 三線相交定共點，叫做“內心”有根源；

點至三邊均等距，可作三角形內切圓， 此圓圓心稱“內心”，如此定義理當然．

五心性質別記混，做起題來真是好。