三角形垂心,指的是三角形的三條高或其延長線相交於一點,這點稱為三角形的垂心。銳角三角形的垂心在三角形內,直角三角形的垂心在直角頂點上,鈍角三角形的垂心在三角形外。
基本介紹
- 中文名:垂心
- 外文名:Orthocenter
- 定義:三角形三條高或其延長線相交一點
- 學科:數學
性質
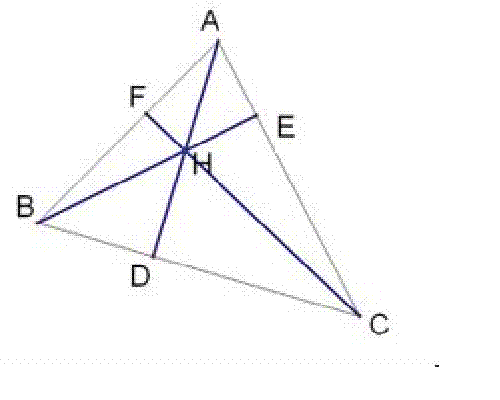 三角形垂心
三角形垂心 三角形的垂心與外心的位置關係
三角形的垂心與外心的位置關係
三角形垂心,指的是三角形的三條高或其延長線相交於一點,這點稱為三角形的垂心。銳角三角形的垂心在三角形內,直角三角形的垂心在直角頂點上,鈍角三角形的垂心在三角形外。
 三角形垂心
三角形垂心 三角形的垂心與外心的位置關係
三角形的垂心與外心的位置關係三角形垂心,指的是三角形的三條高或其延長線相交於一點,這點稱為三角形的垂心。銳角三角形的垂心在三角形內,直角三角形的垂心在直角頂點上,鈍角三角形的垂心在...
三角形的三條高線的交點叫做三角形的垂心。銳角三角形的垂心在三角形內;直角三角形的垂心在直角頂點上;鈍角三角形的垂心在三角形外...
三角形外接圓的圓心叫做三角形的外心。三角形外接圓的圓心也就是三角形三邊垂直平分線的交點,三角形的三個頂點就在這個外接圓上。...
三角形的三條高交於一點。該點叫做三角形的垂心。...... 三角形的三條高交於一點。該點叫做三角形的垂心。其性質包括:1.三角形三個頂點,三個垂足,垂心這7...
三角形五心是指三角形的重心、外心、內心、垂心、旁心。三條中線的交點是重心,三邊垂直平分線的交點是外心,三條內角平分線的交點為內心,三角形三條高線的交點為...
三角形的重心,外心,垂心,內心和旁心稱之為三角形的五心。三角形五心定理是指三角形重心定理,外心定理,垂心定理,內心定理,旁心定理的總稱
垂心:三角形的三條高線的交點叫做三角形的垂心垂心:漢語辭彙...... 垂心:三角形的三條高線的交點叫做三角形的垂心 垂心:漢語辭彙 V百科往期回顧 新手...
垂心等截點(orthocentric isotomic point)是三角形的特殊點之一,即三角形垂心的等截共軛點。三角形的重心、陪位重心與垂心等截點三點共線,且重心到陪位重心的...
四垂心共線作者:夏培貴 引理如圖 1(1)、(2),若AD∥BE,BD∥CE,且AD/BE=BD/CE,則A、B、C三點共線。 這不會有異議,就免去論證。定理完全四邊形中的四...
三角形的四心是指三角形的重心、外心、內心、垂心。若且唯若三角形是正三角形的時候,重心、垂心、內心、外心四心合一心,稱做正三角形的中心。...
僅當三角形是正三角形的時候,重心、垂心、內心、外心四心合一心,稱做正三角形的中心。...
從三角形的一個頂點向它的對邊所在的直線做垂線,頂點到垂足之間的線段叫做三角形的高線,簡稱為三角形的高。...
給定△ABC及其平面上不在三角形邊上的一點P,聯結AP,BP,CP交對應邊於A',B',C',則△A'B'C'稱為P點關於△ABC的切瓦三角形(Cevian Triangle)。...
中點三角形就是把一個三角形的三邊中點順次連線起來的一個新三角形,與原三角形相似。...
三角形的中線是接三角形頂點和它的對邊中點的線段。每個三角形都有三條中線,它們都在三角形的內部。在三角形中,三條中線的交點是三角形的重心。三角形的三條...
定義△ABC的三個歐拉點(頂點與垂心連線的中點)構成的△EAEBEC稱為△ABC的歐拉三角形。它與原三角形關於垂心1:2位似。 有時,歐拉三角形也指球面三角形。 ...
外心是一個數學名詞。是指三角形三條邊的垂直平分線也稱中垂線的相交點。用這個點做圓心可以畫三角形的外接圓。...
旁心,三角形五心之一(其他四個為內心、外心、重心和垂心)。旁心是三角形的旁切圓(與三角形的一邊和其他兩邊的延長線相切的圓)的圓心。...
