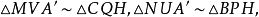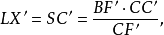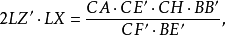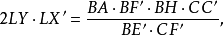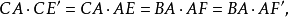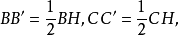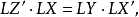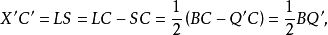基本介紹
- 中文名：垂心等截點
- 外文名：orthocentric isotomic point
- 所屬學科：數學
- 所屬問題：平面幾何（圓）
- 簡介：三角形垂心的等截共軛點
基本概念,相關性質及證明,
基本概念
等截點 在三角形任一邊所在直線上設有兩點與此邊的中點等距，則稱這兩點互為等截點。
等截共軛點 在△ABC中，X、X'、Y、Y'、Z、Z'分別是BC、CA、AB上的等截點，設AX、BY、CZ三線會於一點P，則AX'、BY'、CZ'三線或會於一點P'，或互相平行。當P與P'存在時，它們叫做△ABC的等截共軛點，也說關於△ABC互為等截共軛點。
垂心等截點 垂心的等截共軛點簡稱垂心等截點。
相關性質及證明
①三角形的陪位重心K、重心G、垂心等截點H三者共線，且
(垂心等截點即垂心的等截共軛點)。
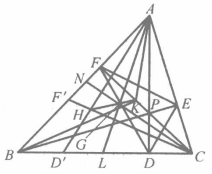圖1證明 如圖1，P是垂心，DE，EF，FD分別是AB，BC，CA的逆平行線；過A，B分別作過EF，FD的中點的直線，則由定理知，其交點為陪位中心K；令D'，F'分別是D，F的等截點，則AD'與CF'的交點H為垂心P的等截點，且K，C，H三點共線，且 。（詳細證明請參見相應參考書籍）。
②證明:三角形的中點三角形，及垂心等截點至三頂點聯結線的中點所連成的三角形，二者的邊相互交於共圓的六點，這圓同為二者的餘弦圓。
圖2證明 如圖，△LMN為△ABC的中點三角形，△A'B'C'為垂心等截點H至三頂點聯結線的中點所連成的三角形，過H作HP // AC，HQ// AB，有
