基本介紹
- 中文名:陪位重心
- 外文名:symmedian point
- 所屬學科:數學
- 所屬問題:平面幾何(三角形)
- 別名:類似重心或勒穆瓦納點
- 簡介:三角形三條陪位中線的交點
基本介紹
陪位中線與陪位重心
相關結論及概念
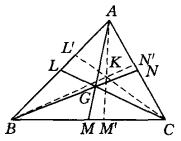 圖1
圖1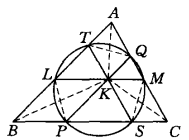 圖2
圖2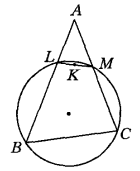 圖3
圖3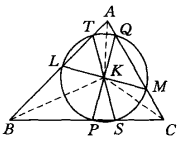 圖4
圖4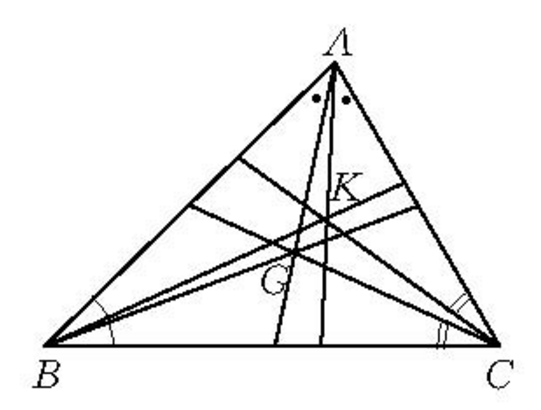
 圖1
圖1 圖2
圖2 圖3
圖3 圖4
圖4陪位重心(symmedian point)亦稱類似重心或勒穆瓦納點,是與三角形重心有關的一個點。三角形三條陪位中線的交點,稱為該三角形的陪位重心,即三角形重心的等角共軛點...
垂心等截點(orthocentric isotomic point)是三角形的特殊點之一,即三角形垂心的等截共軛點。三角形的重心、陪位重心與垂心等截點三點共線,且重心到陪位重心的...
設G是△ABC的重心,K是陪位重心,過K作三邊的平行線l1,l2,l3(圖1),這種平行線稱為勒穆瓦納平行線。圖1 1.三條勒穆瓦納平行線與三角形周界的六個交點在同一...
格雷貝作圖法(Grebe construction method)是求作三角形的陪位重心的一種方法。自三角形△ABC各邊向外作正方形得正方形BCPP′,CAQQ′和ABRR′,設QQ′與RR′,...
三角形的第一Lemoine圓 過三角形陪位重心作三邊的平行線與各邊相交的六個交點共圓。陪位重心:設△ABC的三條中線AM、BN、CL的交點為G(重心),過A作AM'使∠...
布羅卡爾三角形(Brocard triangle)是一些特殊點構成的三角形:1.設S為△ABC的外心,K為它的陪位重心,以SK為直徑作圓,稱這個圓為△ABC的布羅卡爾圓,該圓交三邊...
在三角形中,有三條中線,也有三條陪位中線。於是就有了重心和陪位重心。作一條過兩外兩邊和一邊平行的線。這條線就是這一邊的平行線。並且這條線被中線平分。...
三角形的重心、陪位重心與垂心等截點三點共線,且重心到陪位重心的距離等於重心到垂心等截點距離的一半。等截點等截共軛點 編輯 ...
塔克圓(Tucker circle)是關於幾個點共圓的問題,設K是△ABC的陪位重心,A′,B′,C′各是直線AK,BK,CK上的點,若A′B′∥AB,A′C′∥AC,則B′C′∥BC...
