基本介紹
- 中文名:三角形四心相關定義
- 別稱:三角形的三心
- 提出者:多人
- 提出時間:不詳
- 套用學科:數學
- 適用領域範圍:平面幾何
三角形的外心
垂直性質
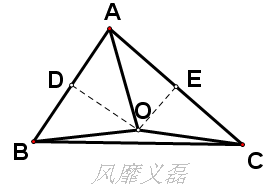 三角形的三條垂直平分線必交於一點
三角形的三條垂直平分線必交於一點外心性質
三角形的內心
證明
 三角形內心
三角形內心性質
三角形的垂心
相交性質
 三角形的三條高必交於一點
三角形的三條高必交於一點垂心性質
三角形的重心

相交性質
 三角形的三條中線必交於一點
三角形的三條中線必交於一點重心性質
三角形的旁心
介紹
旁心的性質
 三角形的旁心(尺規作圖)
三角形的旁心(尺規作圖)歐拉線
證法1
證法2


 三角形的三條垂直平分線必交於一點
三角形的三條垂直平分線必交於一點 三角形內心
三角形內心 三角形的三條高必交於一點
三角形的三條高必交於一點
 三角形的三條中線必交於一點
三角形的三條中線必交於一點 三角形的旁心(尺規作圖)
三角形的旁心(尺規作圖)
三角形的四心是指三角形的重心、外心、內心、垂心。若且唯若三角形是正三角形的時候,重心、垂心、內心、外心四心合一心,稱做正三角形的中心。...
三角形的重心,外心,垂心,內心和旁心稱之為三角形的五心。三角形五心定理是指三角形重心定理,外心定理,垂心定理,內心定理,旁心定理的總稱...
僅當三角形是正三角形的時候,重心、垂心、內心、外心四心合一心,稱做正三角形的中心。...
由不在同一直線上的三條線段首尾順次連線所組成的封閉圖形叫做三角形。 平面上三條直線或球面上三條弧線所圍成的圖形,三條直線所圍成的圖形叫平面三角形;三條...
一、向量的線性運算(10題) 二、向量的數量積(19題) 三、向量的模(6題) 四、向量與三角形的四心(16題) 五、綜合題(47題) 參考答案詞條...
代表作品: 《三角形的“四心”與一組面積關係式》 方亞斌個人簡介 編輯 著有《方亞斌教育教學論文集》,《高中數學複習名師教學與設計》等8部,在《數學通報》等30...
三角形的內角與外角三角形三邊的關係三角形邊與角的關係三角形三邊關係定理的套用三角形角與角間的關係定理的套用(三)三角形的“三線”與“四心”...
三角形的旁切圓(與三角形的一邊和其他兩邊的延長線相切的圓)的圓心,叫做三角形的旁心。...
4.6 三角形的四心模擬檢測四第五講 機率初步5.1 簡單的機率問題5.2 機率的綜合套用模擬檢測五第六講 二次函式6.1 二次函式的圖象及其性質6.2 函式與方程...
第七講 三角形的四心 第八講 函式與幾何 第九講 套用問題 第十講 幾種重要的數學思想方法(三) 答案與提示參考資料 1. 九年級.數學-奧賽急先鋒 .豆瓣...
第17講 三角形的“四心”第18講 圓冪定理第19講 四點共圓問題第20講 圓與圓的位置關係第21講 投影與盲區第22講 三視圖第23講 數形結合...
奧賽習題6-3 §6.4 三角形的“四心” 奧賽習題64 [1] 參考資料 1. 金牌奧賽高分教材:數學(9年級) .京東[引用日期2017-07-10] 2. 金牌奧賽高分教材 數學...
27. 三角形的四心2(44) 28. 正弦定理1(47) 29. 正弦定理2(49) 30. 梅涅勞斯定理1(51) 31. 梅涅勞斯定理2(52) 32. 梅涅勞斯定理3(53) 33. 塞瓦定理...
題型76 向量與三角形的四心……… 117題型77 平面向量的坐標運算……… 118題型78 向量共線(平行)的坐標表示……… 119最有效訓練題21(限時45分鐘) ………...
題型69 向量與三角形的四心題型70 向量的坐標運算題型71 向量平行(共線)的坐標表示第二節 平面向量的數量積題型72 平面向量的數量積...
第八章三角形四心 第八章 三角形四心(解答) 第九章雜題 第九章雜題(解答) 附錄 2004年全國國中數學聯賽試題及答案 2004年全國國中數學競賽試題及答案 第十五屆...
24.三角形的四心150 綜合與拓展 25.拋物線與直線形1——由動點生成的特殊三角形問題157 26.拋物線與直線形2——由動點生成的特殊四邊形問題162 27.拋物線與直線...
第三節 三角形的“四心”第四節 四點共圓第五節 圓的套用性問題第五章 統計與機率第一節 統計第二節 機率第六章 數學思想與解題方法...
第一節 銳角三角函式第二節 解直角三角形第三節 章節複習第六章 圓第一節 圓的基本性質第二節 圓的重要定理第三節 三角形中的四心問題第四節 正多邊形及其...
三角形“四心”的性質及套用[J]. 中學數學, 1993(10). 8. 熊建峰,謝文英. 提煉文章的中心思想[J]. 國小閱讀指南(3-6年級版),2013,(11):12-13. 9. ...
3.1.2相似形 3.2三角形的“四心” 3.3 圓 3.3.1 直線與圓、圓與圓的位置關係 3.3.2點的軌跡 第三部分銜接達標檢測 銜接達標檢測卷 參考答...
和圓的位置關係、與圓有關的計算、與圓有關的綜合題、共圓,共線、圖形的相似(一)、圖形的相似(二)、面積變換、三角形的四心問題、三角函式、解直角三角形等...
第二十講銳角三角函式 第二十一講解直角三角形 第二十二講視圖與投影 第二十三講最值問題 第二十四講三角形四心 第二十五講一元二次方程與二次函...
