三點共線,數學中的一種術語,屬幾何類問題,指的是三點在同一條直線上。可以設三點為A、B、C ,利用向量證明:λAB=AC(其中λ為非零實數)。
相關詞條
- 三點共線
三點共線,數學中的一種術語,屬幾何類問題,指的是三點在同一條直線上。可以設三點為A、B、C ,利用向量證明:λAB=AC(其中λ為非零實數)。...
- 平面向量
若O是三角形ABC的外心,點M滿足OA+OB+OC=OM,則M是三角形ABC的垂心。 若O和三角形ABC共面,且滿足OA+OB+OC=0,則O是三角形ABC的重心。 三點共線:三點A,...
- 孫四周
但是據我們的標識,這6個點組沒有一個顯示為三角形,6個點組仍然還是共線的三點組。第1張照片上的三點共線(共6組)第24張照片中,與第1張照片對應的三點共...
- 歐拉線
∴G是△ABC的重心,即O、H、G三點共線,且GH:GO=AG:GM=2:1歐拉線套用 編輯 1: 平面上共圓的5個點,任取其中3點組成三角形,過其重心作另外兩點連線的...
- 三次曲線
上述性質可以推演出許多射影幾何中有關三點共線(或三線共點)的定理, 如帕斯卡定理、帕普斯定理等等,均可簡易證出。相關人物(2張) 特別的,過一個3x3“籠子”...
- 數學題解辭典(平面解析幾何)
(3)直線過定點(333―338) (4)共線點、共點線(339―345) 12.軌跡題(346―381)數學題解辭典(平面解析幾何)第四章 圓 編輯 1...
- 三角形五心定律
1、三角形三個頂點,三個垂足,垂心這7個點可以得到6個四點圓。 2、三角形外心O、重心G和垂心H三點共線,且OG︰GH=1︰2。(此直線稱為三角形的歐拉線(Euler...
- 無敵每考必出系列:無敵高中數學必背公式
061 三點共線定理 082 線段定比分點的向量公式 083 三角形的重心坐標公式 084 點的平移公式 085 三角形四“心”向量形式的充要條件 必背 不等式 第...
- 幾何
科普中國·科學百科:幾何 3.3萬 53" 用數學在狹窄樓道中“搬”沙發 4.3萬 4' 幾何 [jǐ hé] 科普中國 本詞條由“科普中國”百科科學詞條編寫與套用工...
- 三角形重心定理
三中線交於一點可用燕尾定理證明,十分簡單。(重心原是一個物理概念,對於等厚度...從而向量AO=2/3向量AE, 即向量AO與向量AE共線,所以A、O、E三點共線, 且...
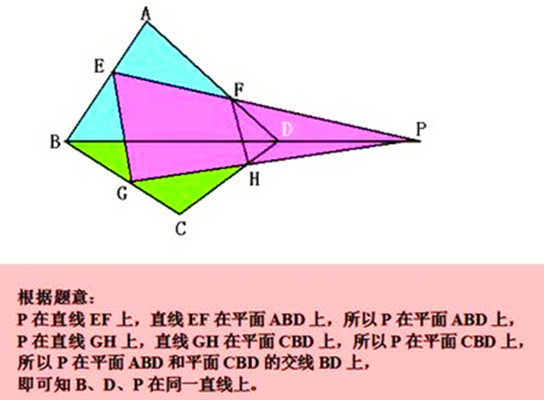
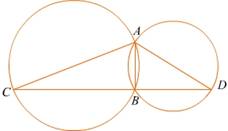 三點共線
三點共線