三點共線,數學中的一種術語,屬幾何類問題,指的是三點在同一條直線上。可以設三點為A、B、C ,利用向量證明:λAB=AC(其中λ為非零實數)。
基本介紹
簡述,證明方法,
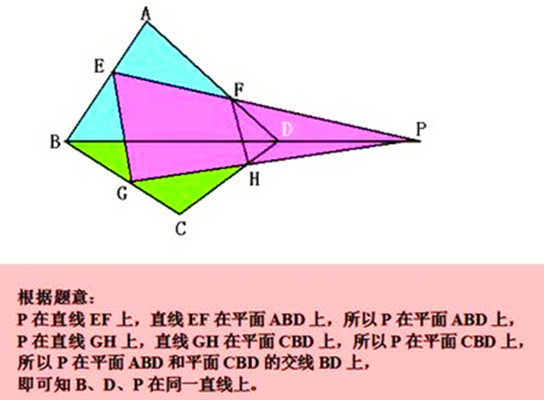
三點共線,數學中的一種術語,屬幾何類問題,指的是三點在同一條直線上。可以設三點為A、B、C ,利用向量證明:λAB=AC(其中λ為非零實數)。
三點共線,數學中的一種術語,屬幾何類問題,指的是三點在同一條直線上。可以設三點為A、B、C ,利用向量證明:λAB=AC(其中λ為非零實數)。...
不妨假設μ≠0,則由 推論1 知,向量a、b共線;這與已知向量a、b不共線矛盾,故假設是錯的,所以λ=μ=0。證畢。共線向量基本定理推論4 如果三點P、A、B...
1、三角形三個頂點,三個垂足,垂心這7個點可以得到6個四點圓。2、三角形外心O、重心G和垂心H三點共線,且OG︰GH=1︰2。(此直線稱為三角形的歐拉線(Euler ...
上述性質可以推演出許多射影幾何中有關三點共線(或三線共點)的定理, 如帕斯卡定理、帕普斯定理等等,均可簡易證出。相關人物(2張) 特別的,過一個3x3“籠子”...
梅涅勞斯逆定理常用來證明三點共線問題,如:笛沙格定理,帕斯卡定理,蝴蝶定理都可用梅涅勞斯定理來證明。 ...
弦長積定理:弧上所有點中,弧的中點到弧兩端的距離乘積最大。 弦長和定理:弧上...即A,P,B'三點共線,AP+BP達到最大值,此時∵點P與點M重合,...
位似變換套用極為廣泛,特別是可以證明三點共線等問題.參考資料 1. 劉新洪.數學書.蘇州:蘇州教育出版社,2008:111 詞條標籤: 科學, 學科 ...
以單張像片為單元,按攝影站、像點及其相應地麵點三點共線原理進行的一種區域網平差。...
三中線交於一點可用燕尾定理證明,十分簡單。(重心原是一個物理概念,對於等厚度...向量BO與向量BF共線,故可設BO=xBF,根據三角形加法法則:向量AO=AB+BO...
