基本介紹
- 中文名:共線向量基本定理
- 別稱:向量共線定理
- 表達式:b=λa
- 套用學科:數學
- 適用領域範圍:幾何
- 適用領域範圍:平面向量
共線向量基本定理
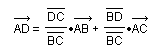
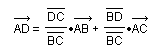
共線向量也就是平行向量,方向相同或相反的非零向量叫平行向量,表示為a∥b ,任意一組平行向量都可移到同一直線上,所以稱為共線向量。共線向量基本定理為如果 a...
如果兩個向量a、b不共線,那么向量p與向量a、b共面的充要條件是:存在唯一實數對x、y,使p=xa+yb。...
共面定理的定義為能平移到一個平面上的三個向量稱為共面向量。共面向量定理是數學學科的基本定理之一。屬於高中數學立體幾何的教學範疇。主要用於證明兩個向量共面...
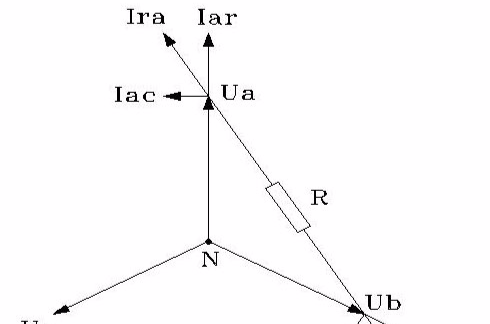
如圖,運用向量證明。 方法一圖片 ∵B、F、A共線,由共線向量基本定理可知,存在唯一實數k,使EF=(1-k)EB+kEA。其中BF=kBA又EF⊥CD...
任作一個向量a,由平面向量基本定理可知,有且只有一對實數x、y,使得: ,我們把(x,y)叫做向量a的(直角)坐標。其中x叫做a在x軸上的坐標,y叫做a在y軸上的...
空間向量基本定理 編輯 1、共線向量定理兩個空間向量a,b向量(b向量不等於0),a∥b的充要條件是存在唯一的實數λ,使a=λb2、共面向量定理...
證明這個定理首先要了解平面向量基本定理:如果E1,E2是同一平面內的兩個不共線向量,那么對於這一平面內的任一向量X,有且只有一對實數A1,A2使X= A1 E1+ A2 ...
10.5 向量共線的條件與軸上向量坐標運算 10.6 平面向量基本定理 10.7 向量的正交分解與向量的直角坐標運算 10.8 向量數量積的物理背景與定義 10.9 向...
5.用平面向量共線基本定理簡解一類題6.介紹兩道類題7.《平面向量》練習題編輯手記 [2] 參考資料 1. 三角與平面向量 .噹噹網[引用日期2019-07-18] 2. ...
向量法證明:設a的方向向量為a,b的方向向量為b,c的方向向量為c,其中a、b、c都是非零向量。∵a∥b∴a∥b由共線向量基本定理可知存在一個唯一實數λ(λ≠0...
二、向量的線性運算三、平面向量基本定理四、平面向量坐標運算核心考點解讀考點一平面向量的概念考點二平面向量的線性運算考點三共線向量定理及其套用...
114 空間向量的線性運算法則 115 共面向量定理 116 空間共線向量定理 117 空間向量基本定理 118 空間向量的坐標運算法則 119 空間向量夾角公式 120 空間...
5平面向量的線性運算 6共線向量定理的套用 7由幾個向量表示某個向量的方法 8以向量為背景的新定義問題 能力測試22 平面向量的基本定理及坐標運算 1平面...
題型72共線向量基本定理及套用109題型73平面向量基本定理及套用109題型74向量與三角形的四心111題型75向量的坐標運算112題型76向量平行(共線)充要條件的...
向量法證明:設a的方向向量為a,b的方向向量為b,面α的法向量為p。∵b⊂α∴b⊥p,即p·b=0∵a∥b,由共線向量基本定理可知存在一實數k使得a=kb...
題型67向量共線的運用題型68 平面向量基本定理及套用題型69 向量與三角形的四心題型70 向量的坐標運算題型71 向量平行(共線)的坐標表示...
113題型72 平面向量的基本概念……… 113題型73 平面向量的線性表示……… 113題型74 向量共線的運用……… 115題型75 平面向量基本定理及套用…...
②掌握向量數乘的運算,並理解其幾何意義,以及兩個向量共線的含義。③了解向量的線性運算性質及其幾何意義。(3)平面向量的基本定理及坐標表示①了解平面向量的基本...
2.3平面向量的基本定理及坐標表示83 一平面向量基本定理83 二兩個向量的夾角84 三平面向量的正交分解及坐標表示85 四平面向量的坐標運算86 五平面向量共線的坐標...
2.3 平面向量的基本定理及坐標表示 2.3.1 平面向量的基本定理及坐標運算 2.3.2 平面向量共線的坐標表示 2.4 平面向量的數量積 2.4.1 平面向量數量積...
題型47 平面向量基本定理的套用題型48 平面向量的坐標表示與運算題型49 平面向量的共線問題題型50 計算平面向量的數量積題型51 平面向量的夾角問題...
