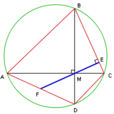
若圓內接四邊形的對角線相互垂直,則垂直於一邊且過對角線交點的直線將平分對邊。
如圖,圓內接四邊形ABCD的對角線AC⊥BD,垂足為M。EF⊥BC,且M在EF上。那么F是AD的中點。
推廣過圓內接四邊形兩對角線交點作任一邊的垂線,必過以其對邊為一邊,以交點為頂點的三角形的外心。
基本介紹
- 中文名:婆羅摩笈多定理
- 外文名:Brahmagupta theorem
- 別稱:布拉美古塔定理
- 提出者:婆羅摩笈多
- 套用學科:數學
- 適用領域範圍:幾何
定理定義,驗證推導,方法一,方法二,定理推廣,證明,方法一,方法二,定理說明,
定理定義
驗證推導
方法一
如圖,運用向量證明。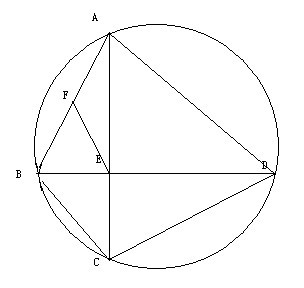 方法一圖片
方法一圖片
 方法一圖片
方法一圖片∵B、F、A共線,由共線向量基本定理可知,存在唯一實數k,使EF=(1-k)EB+kEA。其中BF=kBA
又EF⊥CD
∴EF·CD=[(1-k)EB+kEA]·(CE+ED)=0
展開得(1-k)EB·CE+kEA·CE+(1-k)EB·ED+kEA·ED=0
∵EB⊥CE、EA⊥ED,即EB·CE=0,EA·ED=0
∴kEA·CE+(1-k)EB·ED=0
即k|EA||CE|cos0+(1-k)|EB||ED|cosπ=0
kEA*EC=(1-k)EB*ED
∵EA*EC=EB*ED(相交弦定理)
∴k=1-k,k=1/2
∴BF=1/2*BA,即F是BA中點
方法二
如圖,運用幾何證明。 方法二圖片
方法二圖片
 方法二圖片
方法二圖片∵AC⊥BD,ME⊥BC
∴∠CBD=∠CME
∵∠CBD=∠CAD,∠CME=∠AMF
∴∠CAD=∠AMF
∴AF=MF
∵∠AMD=90°,同時∠MAD+∠MDA=90°
∴∠FMD=∠FDM
∴MF=DF,即F是AD中點
定理推廣
若圓內接四邊形的對角線相互垂直,則一邊中點與對角線交點的連線垂直於對邊。
如上圖,圓內接四邊形ABCD中,AC⊥BD,M是垂足。F是AD中點,則FM⊥BC。
過圓內接四邊形兩對角線交點做另一邊的垂線,必過其對邊為一邊,以交點為一頂點的三角形的外心。
證明
方法一
∵MA⊥MD,F是AD中點

∴AF=MF
∴∠CAD=∠AMF
∵∠CAD=∠CBD,∠AMF=∠CME
∴∠CBD=∠CME
∵∠CME+∠BME=∠BMC=90°
∴∠CBD+∠BME=90°
∴EF⊥BC
方法二
∵F是BA中點

∴EF=1/2*(EA+EB)
CD=CE+ED
EF·CD=1/2*(EA+EB)·(CE+ED)
EF·CD=1/2*(EA·CE+EA·ED+EB·CE+EB·ED)
EF·CD=1/2*(EA*EC-EB*ED)=0
∴EF⊥CD
定理說明
1.此定理是很冷門的(被考即是因為冷門),最好提前引例證明
2.向量法證明是很方便的方法,特別是另一版本的證明,自己想出來的,比我看的任何證明過程都簡單很多
3.想要抓住聯賽的幾何題,類似的冷門定理要多掌握