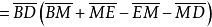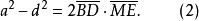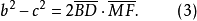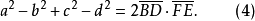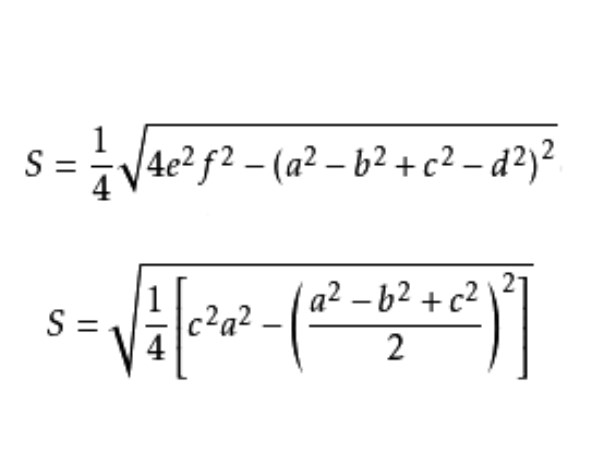布雷特-施奈德公式

布雷特-施奈德公式(Bretschneide formula)是關於四邊形的一個面積公式，也稱貝利契納德(Bretschneider)公式，此公式由Bretschneide(1808~1878)於1842年提出，它是秦九韶的三斜求積公式的推廣。

基本介紹

• 中文名：布雷特-施奈德公式
• 外文名：Bretschneide formula
• 別稱：Bretschneide公式
• 所屬學科：數學（幾何學）
• 簡介：關於四邊形的一個面積公式
• 提出者：Bretschneide

基本介紹

布雷特施奈德公式(Bretschneide formula) 設簡單四邊形的四邊為a、b、c、d，兩對角線為e、f，則面積

若四邊中有一邊退縮為零，上述公式即成秦九韶公式(三斜求積公式)。如當d=0時，則e=c，f=a，

這即秦九韶公式(三斜求積公式)。

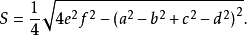
若凸四邊形內接於圓，則ef=ac+bd，於是面積

(此處p為凸四邊形的半周)，後一結論亦稱“婆羅摩笈多定理”。

婆羅摩笈多定理(Brahmagupta theorem)：公元七世紀印度數學家婆羅摩笈多曾經證明了下面兩個定理：（1）如果圓內接四邊形的兩條對角線互相垂直，那么過其交點所作一邊的垂線必將對邊平分；（2）見上述“布雷特施奈德公式”。

Bretschneide公式的證明

Bretschneide公式 若簡單四邊形的四邊長為a、b、c、d，兩對角線長為e.f，則該四邊形的面積為

此公式由Bretschneide(1808~1878)於1842年提出，它是秦九韶的三斜求積公式的推廣。若在上述公式中令d = 0，e = c，f= a，則得到三角形面積公式

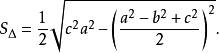
如圖1，簡單四邊形ABCD中，記AB=a,BC= b,CD=c,DA=d,AC=e,BD=f，作CF⊥BD於F，AE⊥BD於E，作CP// BD交AE或其延長線於P，則

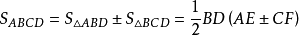
設M是BD的中點，則

即

即

⑵－⑶得

即

所以

比較⑴與⑸式，知