婆羅摩笈多公式

歐氏平面幾何中，婆羅摩笈多公式是用以計算四邊形的面積。它最常用於計算圓內接四邊形面積。

基本形式

婆羅摩笈多公式的最簡單易記的形式，是圓內接四邊形面積計算。若圓內接四邊形的四邊長為a, b, c, d，則其面積為：

其中s為半周長：

證明

圓內接四邊形的面積 = △ADB的面積 + △BDC的面積

但由於ABCD是圓內接四邊形，因此 。故 。所以：（area為四邊形面積）

對△ADB和△BDC利用餘弦定理，我們有：

代入 （這是由於A和C是互補角），並整理，得：

把這個等式代入面積的公式中，得：

它是 的形式，因此可以寫成 的形式：

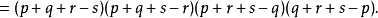
引入 ，

兩邊開平方，得：

證畢。

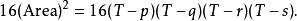
特殊情況

對一般四邊形的面積，擴展的婆羅摩笈多公式用到了四邊形的對角和：

其中θ是四邊形一對角和的一半。（選取另一對角也可以，因其和的一半是π − θ。而因為，所以。)

因為圓內接四邊形的對角和為，而，所以項為零，給出公式的基本形式。

相關定理

海倫公式給出三角形的面積。它是婆羅摩笈多公式取d = 0的特殊情形。

婆羅摩笈多公式的基本形式和擴充形式，就像由勾股定理擴充至餘弦定理一般。