基本介紹
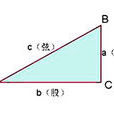
定義




推導
趙爽弦圖

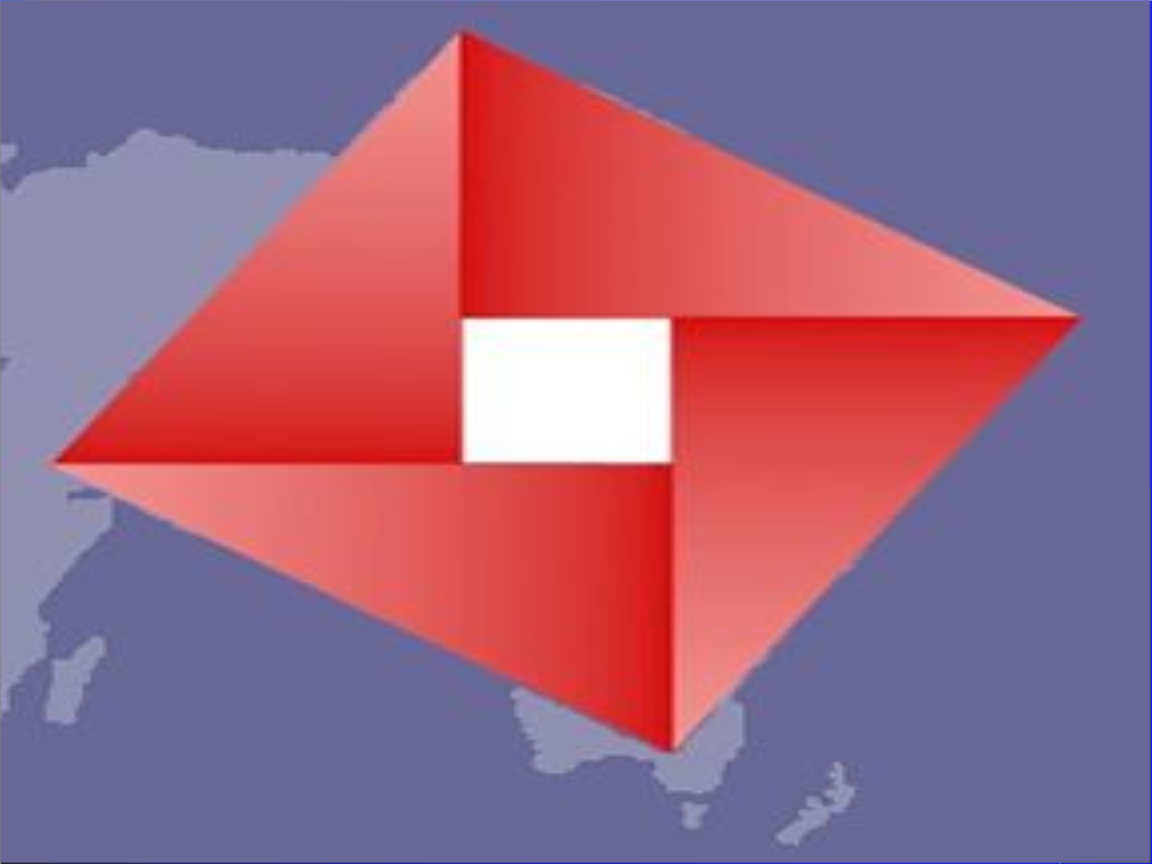 第24屆國際數學家大會會標
第24屆國際數學家大會會標加菲爾德證法






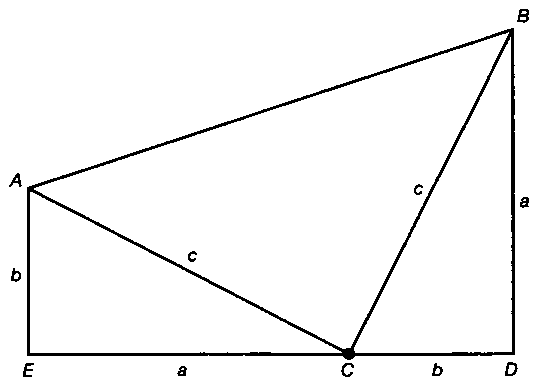 “總統證法”示意圖
“總統證法”示意圖
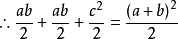


加菲爾德證法變式
 圖示
圖示


青朱出入圖

歐幾里得證法

推廣




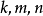






 第24屆國際數學家大會會標
第24屆國際數學家大會會標





 “總統證法”示意圖
“總統證法”示意圖
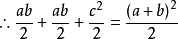


 圖示
圖示









勾股定理是一個基本的幾何定理,指直角三角形的兩條直角邊的平方和等於斜邊的平方。中國古代稱直角三角形為勾股形,並且直角邊中較小者為勾,另一長直角邊為股,...
勾股定理是數學中最重要的定理之一。而勾股圓方圖是由三國時期吳國的數學家趙爽創製,用形數結合的方法,給出了勾股定理的詳細證明。...
小說類型近代現代內容簡介愛情就像三角函數裡的勾股定理,A?+B?C?每個人都是獨立的個體,所以就成為1?+1?2,結局都只能是兩個人…… ...
《千古第一定理:勾股定理》是2009年12月1日高等教育出版社出版的圖書,作者是蔡宗熹。...
勾股數,又名畢氏三元數 。勾股數就是可以構成一個直角三角形三邊的一組正整數。勾股定理:直角三角形兩條直角邊a、b的平方和等於斜邊c的平方(a²+b²=c...
勾股定理又叫畢達哥拉斯定理、商高定理和畢氏定理。在一個直角三角形中,斜邊邊長的平方等於兩條直角邊邊長的平方之和,勾股定理具有無限的魅力,是幾何學中一顆耀眼...
《勾股定理:悠悠4000年的故事》 本書以勾股定理為線索,梳理了科學歷史上一些重要的事件、發明和發現的來龍去脈,把歐幾里得幾何、代數幾何、微積分、黎曼幾何以及...
,如:一條直角邊是a,另一條直角邊是b,如果a的平方與b的平方和等於斜邊c的平方那么這個三角形是直角三角形。(稱勾股定理的逆定理)勾股...
《挑戰思維極限:勾股定理的365種證明》是2016年清華大學出版社出版的圖書,作者是李邁新。...
餘弦定理,歐氏平面幾何學基本定理。餘弦定理是描述三角形中三邊長度與一個角的餘弦值關係的數學定理,是勾股定理在一般三角形情形下的推廣,勾股定理是餘弦定理的特例...
《千古第一定理》是2009年12月1日高等教育出版社出版的一本圖書,作者是蔡宗熹。本書主要講了勾股定理是人類文明史上發揮的作用。...
正餘弦定理指正弦定理和餘弦定理,是揭示三角形邊角關係的重要定理,直接運用它可解決三角形的問題,若對餘弦定理加以變形並適當移於其它知識,則使用起來更為方便、...
“勾股模型”是《夸克模型》之後,由中國閃爍軟體公司“耗散的空虛”領導的專利開發小組對基本粒子的一種表述模型。...
,根據勾股定理,得:此時化簡得出海倫公式,證畢。[2] 海倫公式恆等式 證明:若 ,則證明,如圖:根據恆等式,得:將上面代入,得:④如圖...
畢達哥拉斯還在西方長期被認為是畢達哥拉斯定理(中國稱勾股定理)首先發現者。畢達哥拉斯對數學的研究還產生了後來的理念論和共相論。即有了可理喻的東西與可...
斜邊是指直角三角形中最長的那條邊,也指不是構成直角的那條邊。在勾股定理中,斜邊稱作“弦”。...
軸上的垂直距離 。再次用勾股定理,即證。 [2] 兩點間距離公式極坐標形式 編輯 公式下面不加證明地給出該公式。設極坐標系中兩點 , ,則詞條圖冊 更多圖冊 參考...
直角三角形是一個幾何圖形,是有一個角為直角的三角形,有普通的直角三角形和等腰直角三角形兩種。其符合勾股定理,具有一些特殊性質和判定方法。...
勾股定理(這裡以a,b,c分別代表直角三角形的勾、股、弦三邊之長)a²+b²=C²及其變形b²=c²-a²=(c-a)(c+a),a²=c²-b²=(c-b...
《周髀算經》在數學上的主要成就是介紹了勾股定理。(據說原書沒有對勾股定理進行證明,其證明是三國時東吳人趙爽在《周髀注》一書的《勾股圓方圖注》中給出的)及...
(有一個角是直角),也是特殊的直角三角形(兩條直角邊等),因此等腰直角三角形具有等腰三角形和直角三角形的所有性質(如三線合一、勾股定理、直角三角形斜邊中線定理...
在“勾股圓方圖及注”中他提出用弦圖證明勾股定理和解勾股形的五個公式;在“日高圖及注”中,他用圖形面積證明漢代普遍套用的重差公式,趙爽的工作是帶有開創性的...
