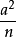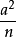定義
一般地,若三角形三邊長a,b,c都是正整數,且滿足a,b的
平方和等於c的平方,那么數組(a,b,c)稱為勾股數組。勾股數組是人們為了解出滿足
勾股定理的
不定方程的所有整數解而創造的概念。
直角三角形兩
直角邊的平方和等於斜邊的平方。如果用a、b和c分別表示直角三角形的兩直角邊和
斜邊,那么a
2+b
2=c
2。
常數
(3n、4n、5n)(n是正整數)(這是最著名的一組!俗稱“勾三,股四,弦五”。古人把較短的
直角邊稱為勾,較長直角邊稱為股,而斜邊則為弦。)
(5n、12n、13n)(n是正整數)
(6、8、10)
(7、24、25)
(8、15、17)
(9、40、41)
(10、24、26)
(11、60、61)
(12、16、20)
(12、35、37)
(13、84、85)
(15、20、25)
(15、112、113)
(17、144、145)
(18、24、30)
(19、180、181)
(20、21、29)
(20、99、101)
(48、55、73)
(60、91、109)
求法
(其實a, +
,
-
,
就是一組萬能的有理數勾股方程,凡是一組勾股數,後面都可以加n的) 例:已知在△ABC中,三邊長分別是a、b、c,a=n2-1,b=2n,c=n2+1(n>1),求證:∠C=90°。
此例說明了對於大於2的任意
偶數2n(n>1),都可構成一組
勾股數,三邊分別是:2n、n
2-1、n
2+1。如:(6、8、10),(8、15、17),(10、24、26) 等。
再來看下面這些勾股數:(3、4、5),(5、12、13),(7、24、25)、(9、40、41),(11、60、61)…這些勾股數都是以
奇數為一邊構成的
直角三角形。由上例已知任意一個大於2的
偶數可以構成一組
勾股數,實際上以任意一個大於1的奇數2n+1(n>1)為邊也可以構成勾股數,其三邊分別是2n+1、2n
2+2n、2n
2+2n+1,這可以通過
勾股定理的逆定理獲證。
a=m2-n2, b=2mn,c=m2+n2,
此處不作討論。
特點
斜邊與奇數邊之差為平方數的2倍
三條邊a,b,c中,兩條邊循環積的4次方之和為平方數,即 a4b4+b4c4+c4a4=L2
三條邊a,b,c的8次方之和為
平方數的2倍,即 a
8+b
8+c
8=2L
2
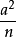 +
+ ,
,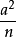 -
- ,就是一組萬能的有理數勾股方程,凡是一組勾股數,後面都可以加n的)
,就是一組萬能的有理數勾股方程,凡是一組勾股數,後面都可以加n的)