基本介紹
公式含義
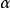
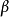

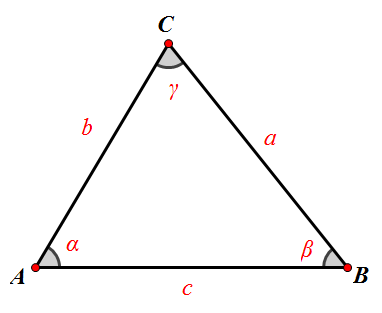 三角形
三角形餘弦定理表達式1
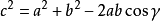

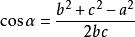


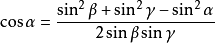
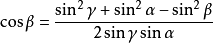
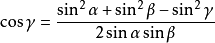
驗證推導
《欽定四庫全書》上的證明
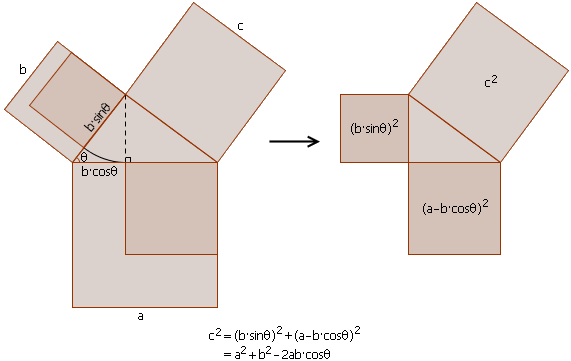 餘弦定理
餘弦定理無字證明
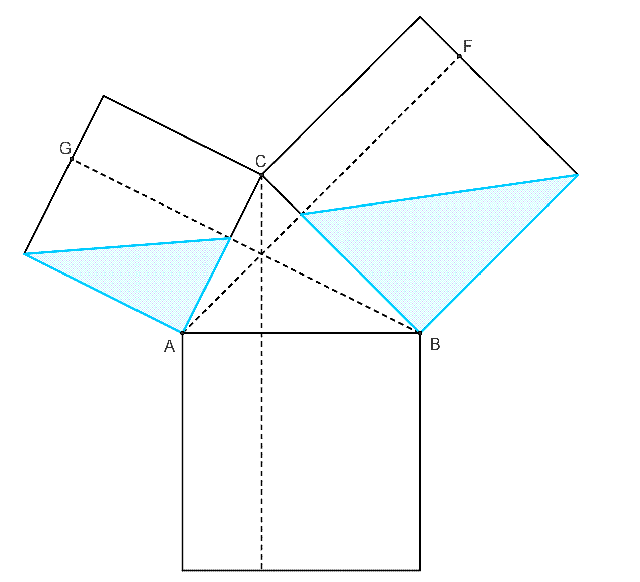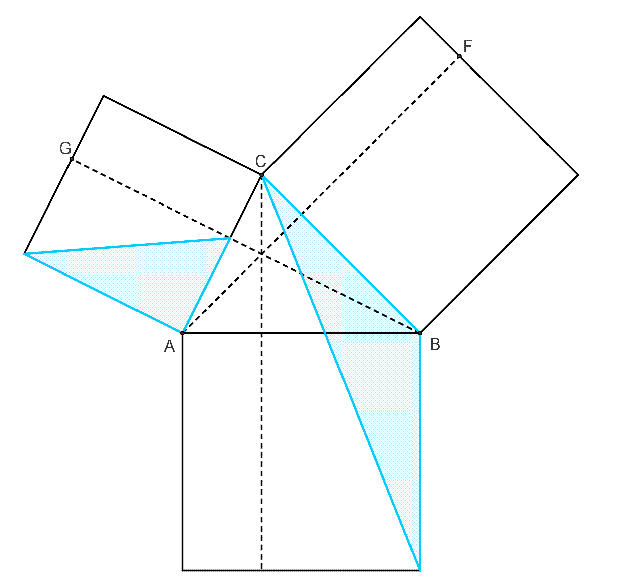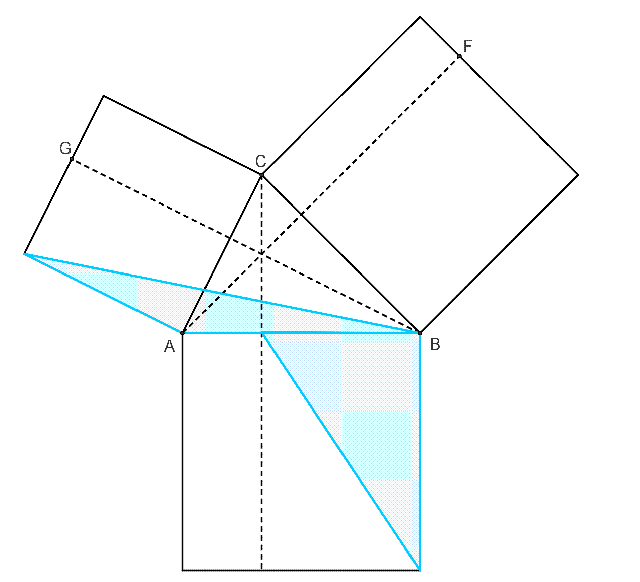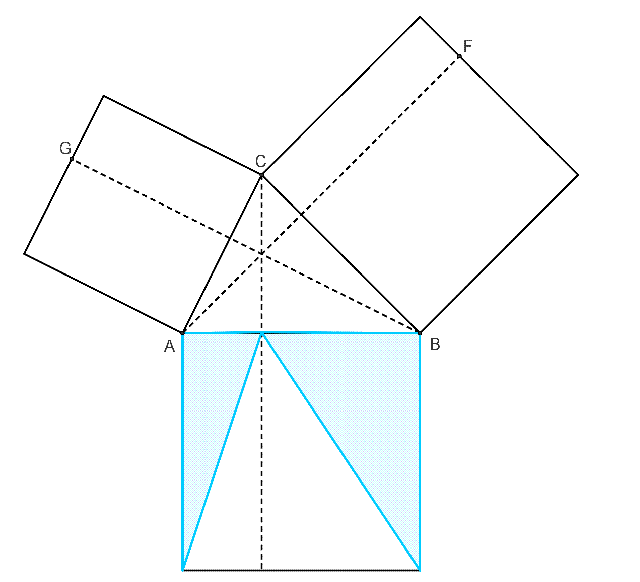 餘弦定理的無字證明
餘弦定理的無字證明平面幾何法證明一
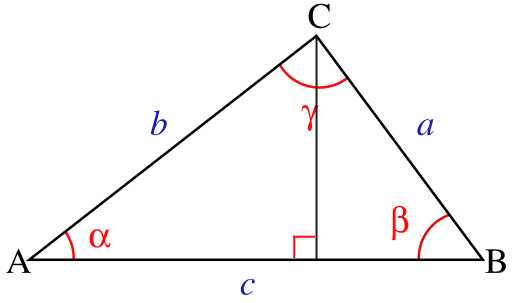 平面幾何法證明
平面幾何法證明

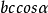
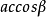
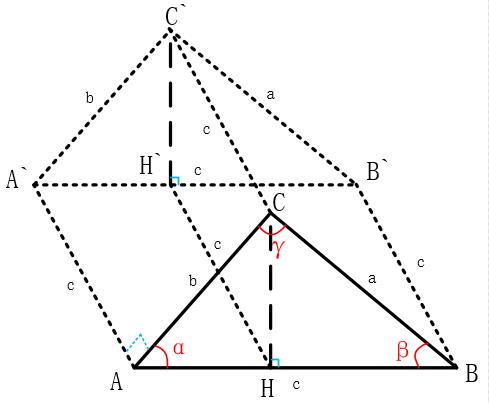 立體幾何輔助說明
立體幾何輔助說明

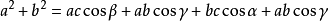



平面幾何法證明二
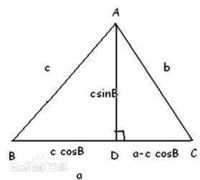 平面幾何法證明二
平面幾何法證明二利用正弦定理證法
平面向量證法
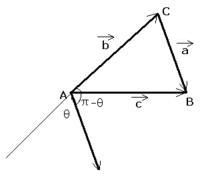 平面向量證法
平面向量證法定理套用
- 當已知三角形的三邊,可以由余弦定理得到三角形的三個內角。
- 當已知三角形的三邊,可以由余弦定理得到三角形的面積。
求邊



求角
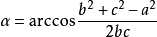

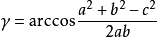
求面積

判定定理
判定定理一 兩根判別法
判定定理二 角邊判別法
套用例題
例如:
再如:

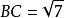

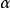
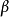

 三角形
三角形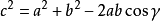

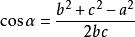


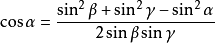
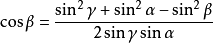
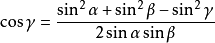
 餘弦定理
餘弦定理 餘弦定理的無字證明
餘弦定理的無字證明 平面幾何法證明
平面幾何法證明

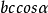
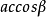
 立體幾何輔助說明
立體幾何輔助說明

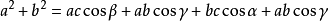



 平面幾何法證明二
平面幾何法證明二 平面向量證法
平面向量證法


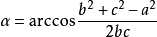

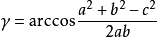


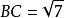
餘弦定理,歐氏平面幾何學基本定理。餘弦定理是描述三角形中三邊長度與一個角的餘弦值關係的數學定理,是勾股定理在一般三角形情形下的推廣,勾股定理是餘弦定理的特例...
正餘弦定理指正弦定理和餘弦定理,是揭示三角形邊角關係的重要定理,直接運用它可解決三角形的問題,若對餘弦定理加以變形並適當移於其它知識,則使用起來更為方便、...
射影定理,又稱“歐幾里德定理”:在直角三角形中,斜邊上的高是兩條直角邊在斜邊射影的比例中項,每一條直角邊又是這條直角邊在斜邊上的射影和斜邊的比例中項...
餘弦(餘弦函式),三角函式的一種。在Rt△ABC(直角三角形)中,∠C=90°(如圖所示),∠A的餘弦是它的鄰邊比三角形的斜邊,即cosA=b/c,也可寫為cosa=AC/AB。...
三面角餘弦定理證明 將三面角O-ABC的頂點與單位球的球心重合,並設三邊與球面分別交於A、B、C。根據球面三角形的定義,在球面△ABC中,∠AOB=c,∠BOC=a,∠...
四邊形餘弦定理是由三角形餘弦定理推廣得到的定理cosθ=(a^2+c^2-b^2-d^2)/2AC*BD...... 四邊形餘弦定理是由三角形餘弦定理推廣得到的定理 cosθ=(a^2...
正弦定理(The Law of Sines)是三角學中的一個基本定理,它指出“在任意一個平面三角形中,各邊和它所對角的正弦值的比相等且等於外接圓的直徑”,即a/sinA = ...
該定理從老版高中教材人教版《數學》必修第二冊(下A),P35的例1:“河堤斜面與水平面所成的二面角為60°,堤面上有一條直道CD,它與堤腳水平線AB的夾角為30°...
最小角定理(minimum angle theorem)是立體幾何的重要定理之一,指與平面斜交的直線與它在該平面內的射影的夾角不大於直線與平面內其他直線的夾角。...
半角定理指的是已知一個三角形的三個邊長,從而可求出各個角的半角的正切值,並由此可出各個角和此三角形的內切圓半徑的公式。...
詳見詞條:餘弦定理餘弦定理 對於如圖所示的邊長為a、b、c而相應角為α、β、γ的△ABC,有:也可表示為:三角函式公式降冪公式 sin²α=[1-cos(2α)]/2...
一般地,把三角形的三個角A,B,C和它們的對邊a,b,c叫做三角形的元素。已知三角形的幾個元素求其他元素的過程叫做解三角形。解三角形,常用到正弦定理和餘弦定理...
交角公式是計算角的一種公式,設點Pi的直角坐標為(xi,yi)(i=0,1,2),則以射線P0P1與P0P2為邊的角θ∈(0,π)可由餘弦定理而得。可以從兩向量的夾角思考...
三角定律,簡單的說就是五條數學定律。正弦定理,餘弦定理,直角三角形中的射影定理,大角對大邊定理,內角平分線定理。...
直角三角形射影定理,又稱“歐幾里德定理”,定理內容是直角三角形中,斜邊上的高是兩直角邊在斜邊上射影的比例中項,每一條直角邊是這條直角邊在斜邊上的射影和...
11 相關定理 ▪ 解釋 ▪ 正弦定理 ▪ 餘弦定理 ▪ 正切定理 ▪ 廣義射影定理 ▪ 三角恆等式 12 函式介紹 ▪ 正弦函式 ▪ 餘弦函式...
