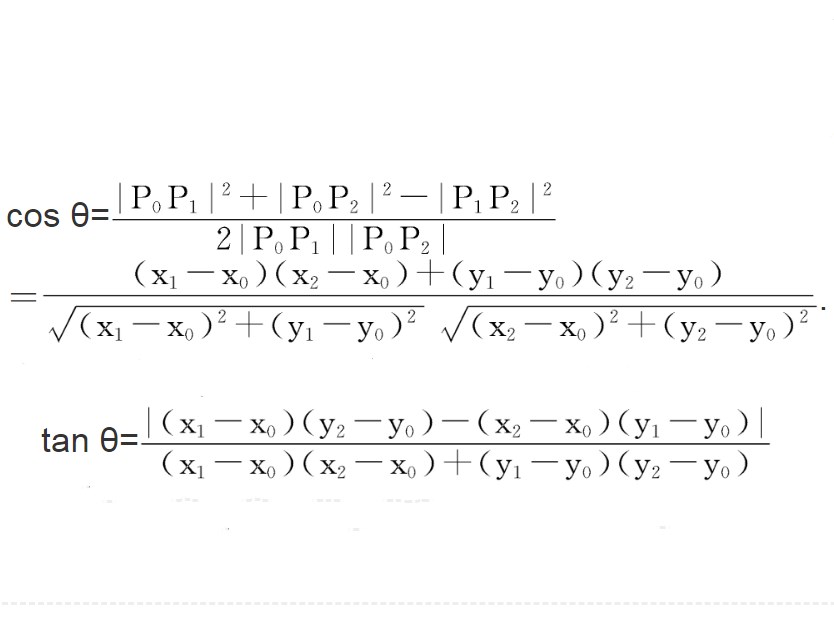基本介紹
- 中文名:交角公式
- 所屬學科:數學
- 所屬問題:向量和三角函式
- 相關概念:餘弦定理,兩向量的夾角
基本介紹,相關介紹,兩向量的夾角,內積的性質,
基本介紹
交角公式的依據——餘弦定理 餘弦定理是關於三角形邊角關係的重要定理之一。該定理斷言:三角形任一邊的平方等於其他兩邊平方和減去這兩邊與它們夾角的餘弦的積的兩倍。若a,b,c分別表示△ABC中A,B,C的對邊,則餘弦定理可表述為:

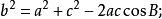
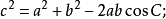
餘弦定理還可以用以下形式表達:
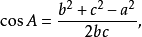


交角公式設點Pi的直角坐標為(xi,yi)(i=0,1,2),則以射線P0P1與P0P2為邊的角θ∈(0,π)可由餘弦定理(也可以從兩向量的交角的角度去思考)而得
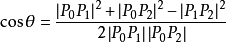


相關介紹
兩向量的夾角
設有兩個非零向量a,b,任取空間一點O,作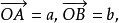 設φ=∠AOB,規定0≤φ≤π,則φ稱為向量a與b的夾角。通常記作
設φ=∠AOB,規定0≤φ≤π,則φ稱為向量a與b的夾角。通常記作
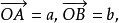

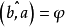
向量的夾角是平面或空間中兩非零向量間的夾角.設a,b是兩個非零向量,自任意一點O作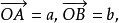 則由射線OA和OB構成的角稱為向量a與b的夾角,記為∠(a,b)。若a與b同向,則∠(a,b)=0;若a與b反向,則∠(a,b)=π;若a與b不平行,則∠(a,b)∈(0,π)。在空間直角坐標系中,已知向量a=(a1,a2,a3),b=(b1,b2,b3),那么這兩向量的夾角∠(a,b)可由下式惟一確定:
則由射線OA和OB構成的角稱為向量a與b的夾角,記為∠(a,b)。若a與b同向,則∠(a,b)=0;若a與b反向,則∠(a,b)=π;若a與b不平行,則∠(a,b)∈(0,π)。在空間直角坐標系中,已知向量a=(a1,a2,a3),b=(b1,b2,b3),那么這兩向量的夾角∠(a,b)可由下式惟一確定:
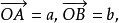
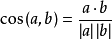
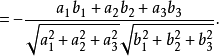
零向量與任一向量的夾角不確定。
內積的性質
1.e是單位向量,則e·a=a·e=|a|cos<a,e>
2.a⊥b⇔a·b=0(a,b為非零向量);
3.a·a=|a|或|a|= ;
;

4.cos<a,b>=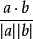 ;
;
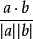
5.|a·b|≤|a||b|;
說明:(1)兩個向量的數量積不同於它們的加減運算或數乘,其結果不是向量而實數,它的符號由兩向量的夾角的餘弦來決定.
注意規定a·0=0。
(2)關於數量積的運算律,一定要注意以下幾點:
①a=0,則a·b=0,但是由a·b=0,不能得到a=0或b=0.因為a⊥b時,a·b=0;
②a=c時,a·b=c·b,但是由a·b=c·b,不能得到a=c,即消去律不成立;
③(a·b)c≠a(b·c),因為(a·b)c與c平行,a(b·c)與a平行,一般地,a,c不共線,故(a·b)c≠a(b·c)。
(3)數量積在處理有關長度、角度、垂直問題方面有重要的作用,應充分注意下列三個公式.
①|a|= ,這是處理與長度(距離)有關問題的依據;
,這是處理與長度(距離)有關問題的依據;

②cosθ=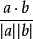 ,這是求角的主要依據;
,這是求角的主要依據;
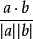
③a·b=0⇔a⊥b(a,b為非零向量),這是判定垂直的主要依據,套用時要注意非零向量這個條件。