基本介紹
- 中文名:正弦定理
- 外文名:The Law of Sines
- 表達式:a:b:c=sinA:sinB:sinC
- 提出者:納綏爾丁
- 提出時間:公元10世紀
- 套用學科:數學
- 適用領域範圍:三角函式
- 突出貢獻著:韋達、海倫、秦九韶
發展簡史
定理定義

驗證推導



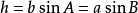





















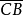





















定理意義
- 已知三角形的兩角與一邊,解三角形。
- 已知三角形的兩邊和其中一邊所對的角,解三角形。
- 運用a:b:c=sinA:sinB:sinC解決角之間的轉換關係。
定理推廣












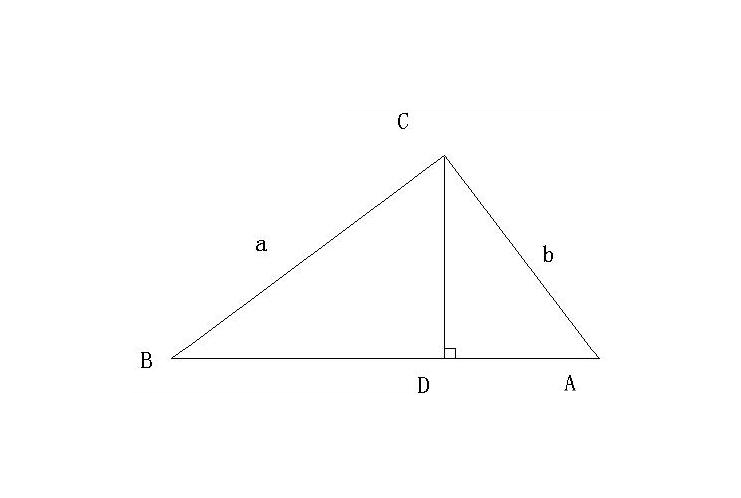




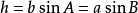





















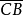

































正弦定理(The Law of Sines)是三角學中的一個基本定理,它指出“在任意一個平面三角形中,各邊和它所對角的正弦值的比相等且等於外接圓的直徑”,即a/sinA = ...
餘弦定理,歐氏平面幾何學基本定理。餘弦定理是描述三角形中三邊長度與一個角的餘弦值關係的數學定理,是勾股定理在一般三角形情形下的推廣,勾股定理是餘弦定理的特例...
正弦(sine),數學術語,在直角三角形中,任意一銳角∠A的對邊與斜邊的比叫做∠A的正弦,記作sinA(由英語sine一詞簡寫得來),即sinA=∠A的對邊/斜邊。古代說法,...
正弦公式是描述正弦定理的相關公式,而正弦定理是三角學中的一個基本定理,它指出:在任意一個平面三角形中,各邊和它所對角的正弦值的比相等且等於外接圓的直徑。...
正餘弦定理指正弦定理和餘弦定理,是揭示三角形邊角關係的重要定理,直接運用它可解決三角形的問題,若對餘弦定理加以變形並適當移於其它知識,則使用起來更為方便、...
拉密原理(Lami's theorem):在同一平面內,當三個共點力的合力為零時,其中任意一個力與其它兩個力夾角正弦的比值相等,即F1/sinα=F2/sinβ=F3/sinγ。其...
角平分線定理1是描述角平分線上的點到角兩邊距離定量關係的定理,也可看作是角平分線的性質。角平分線定理2是將角平分線放到三角形中研究得出的線段等比例關係的...
維維安尼定理:正三角形(等邊三角形)內或邊界上任一點到三邊的距離之和為定值,這定值等於該三角形的高。...
也就是說,利用該定理可以很方便地求出異面直線所成角。三餘弦定理定理套用 編輯 如果將三餘弦定理和三正弦定理聯合起來使用,用於解答立體幾何綜合題,你會發現出乎...
正弦定理變形可得:三角函式公式餘弦定理 詳見詞條:餘弦定理餘弦定理 對於如圖所示的邊長為a、b、c而相應角為α、β、γ的△ABC,有:也可表示為:...
一般地,把三角形的三個角A,B,C和它們的對邊a,b,c叫做三角形的元素。已知三角形的幾個元素求其他元素的過程叫做解三角形。解三角形,常用到正弦定理和餘弦定理...
三角定律,簡單的說就是五條數學定律。正弦定理,餘弦定理,直角三角形中的射影定理,大角對大邊定理,內角平分線定理。...
