基本介紹
- 中文名:弦長定理
- 外文名:The Chords' Length Theorem
- 提出者:With an Orchid
- 提出時間:2019年08月10日
- 套用學科:數學
- 適用領域範圍:數學
定律定義







推導過程
弦長積定理





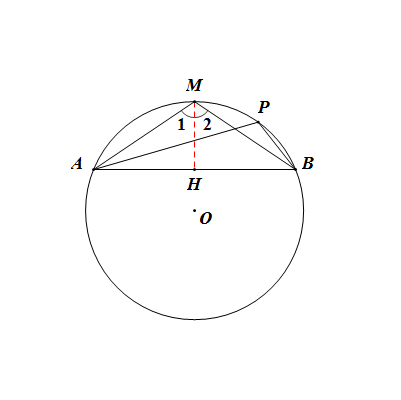
















弦長和定理














 弦長和定理 證法二
弦長和定理 證法二








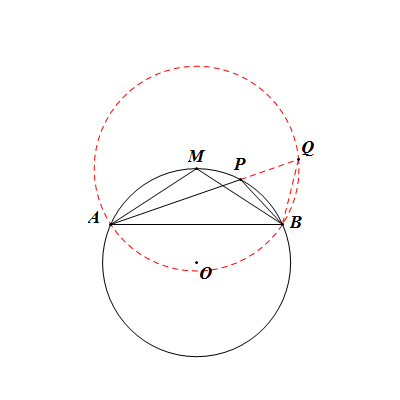
 弦長和定理 證法三 圖①
弦長和定理 證法三 圖①

 弦長和定理 證法三 圖②
弦長和定理 證法三 圖②發展簡史













































 弦長和定理 證法二
弦長和定理 證法二








 弦長和定理 證法三 圖①
弦長和定理 證法三 圖①

 弦長和定理 證法三 圖②
弦長和定理 證法三 圖②
弦長公式,在這裡指直線與圓錐曲線相交所得弦長d的公式。PS:圓錐曲線, 是數學、幾何學中通過平切圓錐(嚴格為一個正圓錐面和一個平面完整相切)得到的一些曲線,如:...
弦長定理是弦長積定理與弦長和定理的合稱。弦長積定理:弧上所有點中,弧的中點到弧兩端的距離乘積最大。弦長和定理:弧上所有點中,弧的中點到弧兩端的距離之和最...
定理內容:弧上的所有點中,弧的中點到弧兩端距離和最長。...... 定理內容:弧上的所有點中,弧的中點到弧兩端距離和最長。中文名 弦長和定理 外文名 Chords' ...
前後緣的距離稱為弦長。如果機翼平面形狀不是長方形,一般在參數計算時採用製造商指定位置的弦長或平均弦長...
德古阿定理是勾股定理的三維形式,以法國數學家讓·保羅·德古阿·德馬爾弗(Jean Paul de Gua de Malves)命名。...
載荷弦長指板彈簧承受載荷時的弦長。...... 載荷弦長指板彈簧承受載荷時的弦長。中文名稱 載荷弦長 英文名稱 span under load 定義 板彈簧承受載荷時的弦長。 應...
圓錐曲線硬解定理,又稱CGY-EH定理(The CGY Ellipse & Hyperbola Theorem)或JZQ-EH定理(The JZQ Ellipse & Hyperbola Theorem),其實是一套求解橢圓(或雙曲線)與...
Dra式第一定理簡單來說就是弧平分弦,其揭示了兩特殊位置相交的圓的弧弦關係。...... 定理定義在圓1上作任意一弦,以其一端點為圓心,弦長為半徑作圓2。在圓1...
舒爾定理(Schur theorem)關於平面曲線的一個定理.它是描述平面曲線在無伸縮的彎曲下性態變化的...
門納勞斯定理(Menelaus theorem)是關於共線點的一個重要定理,設X,Y,Z分別是△ABC三邊BC,CA,AB或其延長線上的點,則它們共線的必要充分條件是(XB/XC)·(YC/...
虛空之弦長弓是魔獸系列遊戲世界中的一件武器...... 虛空之弦長弓是魔獸系列遊戲世界中的一件武器 中文名稱 虛空之絃長弓 類型 遠程 物品來源 風暴要塞 需要等...
1 圓的弦 ▪ 定義 ▪ 圓的相交弦定理 ▪ 相交弦定理證明 ▪ 圓的弦長的計算 2 概念推廣 3 三角形的弦 ▪ 定義 ▪ 勾股定理 弦...
焦點弦長就是這兩個 焦半徑長之和。⑴過橢圓焦點F的直線交橢圓於A、B兩點,...定理3 橢圓、雙曲線、拋物線焦點的極線是相應的準線。定理4 如果橢圓、雙曲線...
