Dra式第一定理簡單來說就是弧平分弦,其揭示了兩特殊位置相交的圓的弧弦關係。
基本介紹
- 中文名:Dra氏第一定理
- 外文名:Dra theorem
- 別稱:Zhuai(一聲)氏定理、拽一
- 表達式:AC=BC
- 套用學科:數學
- 適用領域範圍:數學
- 適用領域範圍:物理
定理定義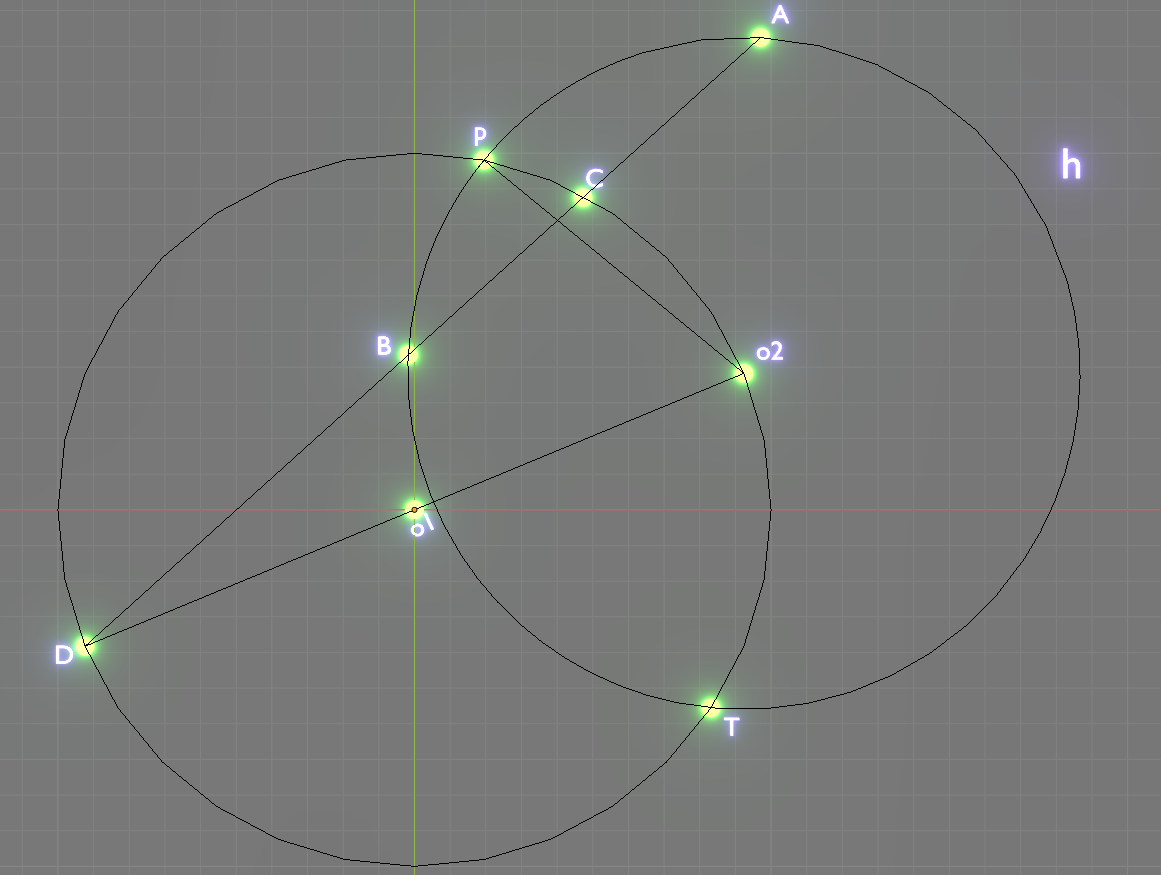

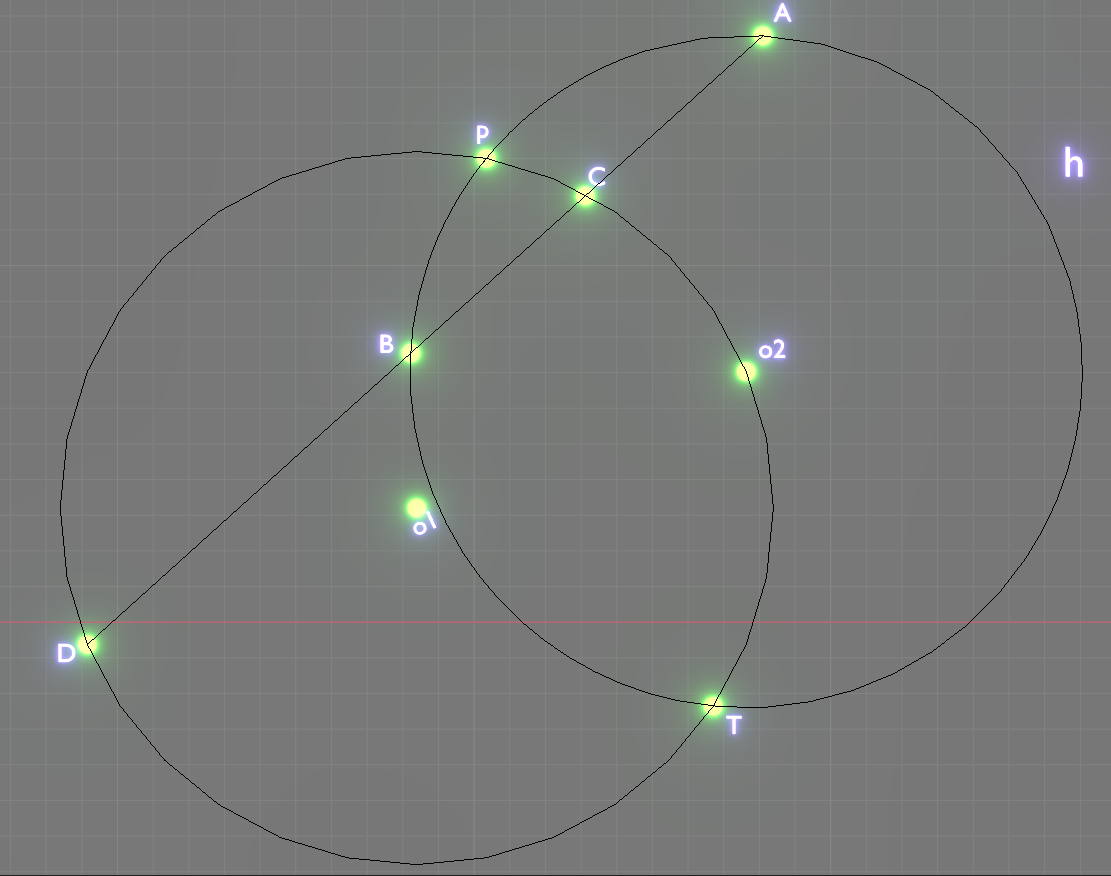
在圓1上作任意一弦,以其一端點為圓心,弦長為半徑作圓2。在圓1外的圓2弧上任取一點,連線圓1與圓2圓心連線延長線交圓1弧的交點,那么這兩點的連線所截圓2產生的弦總是被圓1在圓2內部分的弧所平分。
設圓一O1,在弧上任取一弦P-O2,以P-O2為半徑,O2為圓心作圓O2(兩圓另一交點為T)。延長線段O1-O2,交圓O1於點D。在弧PhT上任取一點A,連線A、D交圓O1於點C,且交圓O2於點B,那么線段AD截圓O2的弦——AB被弧P-O2-T與其的交點C所平分,即AC=BC。
證明
連線A-O2與B-O2,連線C-O2。

∵D-O2為圓O1直徑,且點C在圓O1上 ∴∠D-C-O2為直角,即C-O2⊥AB
又∵B-O2與A-O2為圓O2的半徑∴B-O2=A-O2 ∴AC=BC(三線合一)
∵點C總在O1上 ∴ ∠D-C-O2總為直角 ∴總有三線合一∴總有AC=BC