圓錐曲線硬解定理,又稱CGY-EH定理(The CGY Ellipse & Hyperbola Theorem)或JZQ-EH定理(The JZQ Ellipse & Hyperbola Theorem),其是一套求解橢圓(或雙曲線)與直線相交時,聯立方程求判別式、韋達定理與相交弦長的簡便算法,常套用於解析幾何。
基本介紹
- 中文名:圓錐曲線硬解定理
- 外文名:CGY-EH & JZQ-EH
- 別稱:CGY-EH定理
- 提出者:CGY(2010) & 136266943(2014)
- 提出時間:2010 & 2014
- 套用學科:中學數學
- 適用領域範圍:標準雙曲線與橢圓
- 適用領域範圍:標準圓錐曲線
定理簡介,定理內容,定理說明,定理補充,定理簡證,
定理簡介
在將圓錐曲線的方程與直線方程聯立求解時人們發現了可消項的存在。但其一般化的推導結果不具有普適性,且一直無法用一個簡潔的形式表示.。由CGY(2010)以橢圓曲線推導,重新排列分組形式,並引入ε,從而得出了較為簡潔的表示形式。後再由CGY成功引入弦長計算公式,並將適用範圍擴大到對y值求解與對x的求解,從而奠定了CGY-EH定理強大的通用性與普適性。
定理內容
若曲線 與直線
與直線 相交於
相交於 兩點,則:
兩點,則:







其中 ;
; 。
。


定理說明
套用該定理於
①橢圓時:
焦點位x軸時: ,應將
,應將 代入。
代入。


焦點位於y軸時: ,應將
,應將 代入。
代入。


②雙曲線時:
焦點位於x軸時: ,應將
,應將 代入,同時
代入,同時 不應為零,即
不應為零,即 不為零;
不為零;




焦點位於y軸時: ,應將
,應將 代入,同時
代入,同時 不應為零,即
不應為零,即 不為零
不為零




求解 與
與 時,只須將
時,只須將 與
與 的值互換且
的值互換且 與
與 的值互換。可知
的值互換。可知 與
與 的值不會因此而改變。
的值不會因此而改變。








定理補充
聯立曲線方程與
 是現行高考中比聯立
是現行高考中比聯立 更為普遍的現象。其中聯立後的二次方程是標準答案中必不可少的一項,
更為普遍的現象。其中聯立後的二次方程是標準答案中必不可少的一項, ,
, 都可以直接通過韋達定理求得,唯獨弦長的表達式需要大量計算。這裡給出一個CGY-EH的斜率式簡化公式,以減少記憶量,以便在考試中套用。
都可以直接通過韋達定理求得,唯獨弦長的表達式需要大量計算。這裡給出一個CGY-EH的斜率式簡化公式,以減少記憶量,以便在考試中套用。





若曲線 與直線:
與直線: 相交於
相交於 兩點,則:
兩點,則:





這裡的 既可以是常數,也可以是關於
既可以是常數,也可以是關於 的代數式。
的代數式。


由這個公式我們可以推出:
若曲線 為橢圓:
為橢圓:
 ,則
,則




若曲線 為雙曲線:
為雙曲線: ,則
,則



由於在高考中CGY-EH定理不可以直接套用,因此現提供參考解題步驟:
解:
由 ,得
,得



設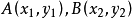
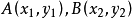
由韋達定理,得:
 ①,
①,
 ②;
②;




由 ,代入①②式,化簡得:
,代入①②式,化簡得:


所以

注:對於橢圓:
 與直線:
與直線: ,聯立得:
,聯立得:




對於雙曲線:
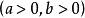 與直線:
與直線: ,聯立得:
,聯立得:

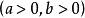


定理簡證
設曲線: (mn
(mn 0,且m,n不同時為負數)與直線:
0,且m,n不同時為負數)與直線:
 相交於E、F兩點,聯立兩式,得二次方程:
相交於E、F兩點,聯立兩式,得二次方程:






根據韋達定理,得:


由於 的意義僅在於正負性,且
的意義僅在於正負性,且 恆成立,可令
恆成立,可令 ,則
,則 與
與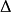 同號
同號




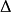
由

(或 )
)

可得

令 ,則可得CGY-EH定理:
,則可得CGY-EH定理:






