起源 2000多年前,古希臘數學家最先開始研究圓錐曲線,並獲得了大量的成果。古希臘數學家
阿波羅尼斯 採用平面切割圓錐的方法來研究這幾種曲線。用垂直於錐軸的平面去截
圓錐 ,得到的是
圓 ;把平面漸漸傾斜,得到
橢圓 ;當平面傾斜到“和且僅和”圓錐的一條
母線 平行時,得到
拋物線 ;用平行於圓錐的軸的平面截取,可得到雙曲線的一支(把圓錐面換成相應的二次錐面時,則可得到
雙曲線 )。
阿波羅尼 曾把橢圓叫“虧曲線”,把雙曲線叫做“超曲線”,把拋物線叫做“齊曲線”。事實上,阿波羅尼在其著作中使用純幾何方法已經取得了今天高中數學中關於圓錐曲線的全部性質和結果。
定義 幾何觀點
用一個平面去截一個
二次錐面 ,得到的
交線 就稱為圓錐曲線(conic sections)。
通常提到的圓錐曲線包括橢圓,雙曲線和拋物線,但嚴格來講,它還包括一些退化情形。具體而言:
1) 當平面與
二次錐面 的母線平行,且不過圓錐頂點,結果為拋物線。
2) 當平面與
二次錐面 的母線平行,且過圓錐頂點,結果退化為一條直線。
3) 當平面只與
二次錐面 一側相交,且不過圓錐頂點,結果為橢圓。
4) 當平面只與
二次錐面 一側相交,且不過圓錐頂點,並與圓錐的對稱軸垂直,結果為圓。
5) 當平面只與
二次錐面 一側相交,且過圓錐頂點,結果為一點。
6) 當平面與
二次錐面 兩側都相交,且不過圓錐頂點,結果為雙曲線(每一支為此
二次錐面 中的一個圓錐面與平面的交線)。
7) 當平面與
二次錐面 兩側都相交,且過圓錐頂點,結果為兩條相交直線。
注意,上述曲線類中不含有二次曲線:兩平行直線。
代數觀點
在笛卡爾平面上,二元二次方程
的圖像稱為二次曲線。根據
判別式 的不同,包含了橢圓、雙曲線、拋物線以及各種退化情形。
焦點--準線及其推廣觀點
傳統的焦點-準線統一定義
給定一點P,一直線L以及一非負實常數e,則到P的距離與L距離之比為e的點的軌跡是圓錐曲線。
根據e的範圍不同,曲線也各不相同。具體如下:
1) e=0,軌跡為一點或一個圓;
2) e=1(即到P與到L距離相同),軌跡為拋物線;
4) e>1,軌跡為雙曲線。
2.一、二次曲線的統一定義
(《
數學通報 》2016.12期《一、二次曲線的軌跡統一及性質》一文中,我國中學數學教師
胡新平 將焦點--準線進行了推廣,從而可以給出以下完整的一、二次曲線的統一定義)
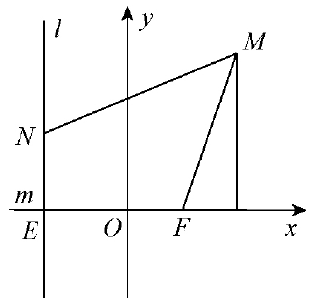
平面上有兩條互相垂直且相交於點E的直線l,m,點F是直線m上的一定點,|EF|=p,點N 是直線l上一動點,軌跡動點M同時滿足下列兩條件:
(Ⅰ)動點N與動點M到定直線m的有向距離Nm與Mm有
圖片3 Nm=(1+t)Mm,其中t為實常數;
(Ⅱ)動點M到定點F的距離|MF|與到動點N的距離|MN|有
|MF|=e|MN|,其中e為非負常數,
則在直角坐標變換觀點下,動點M的軌跡是一、二次曲線
(約定e=1,t =1,p=0不同時成立).
點 M 的軌跡具體情形如下:
(A)p≠0時:含六類一、二次曲線類.
e≠0時,
(1)當e=1,|t|=1 時,軌 跡 是 一 條 一 重直線;
(2)當e=1,|t|≠1時,軌跡是拋物線;
圖1 (3)當e<1,e|t|<1, 或e>1,e|t|>1時,軌跡是橢圓.其中|t|=1時是圓;
(4)當e≠1,e|t|=1 時,軌 跡 是 兩 條 平 行直線;
(5)當e<1,e|t|>1時,或e>1,e|t|<1時,軌跡是雙曲線;
e=0時,軌跡是一點
(B)p=0時:含三類一、二次曲線類.
(1)當e<1,e|t|>1時,或e>1,e|t|<1時,軌跡是兩條相交直線;
(2)當e=1,e|t|≠1時,或e≠1,e|t|=1時,軌跡是兩條重合直線;
(3)當e<1,e|t|<1,或e>1,e|t|>1時,軌跡是一點.
稱其中的定點F 和定直線l為對應軌跡曲線 的擬焦點和與擬焦點F相應的擬
準線 .
概念 (以下以純幾何方式敘述主要的圓錐曲線通用的概念和性質,由於大部分性質是在焦點-準線觀點下定義的,對於更一般的退化情形,有些概念可能不適用。)
考慮焦點--準線觀點下的圓錐曲線定義。定義中提到的定點,稱為圓錐曲線的
焦點 ;定直線稱為圓錐曲線的
準線 ;固定的常數(即圓錐曲線上一點到
焦點 與
準線 的距離比值)稱為圓錐曲線的
離心率 ;焦點到準線的距離稱為
焦準距 ;焦點到曲線上一點的
線段 稱為
焦半徑 。過焦點、平行於準線的直線與圓錐曲線相交於兩點,此兩點間的線段稱為圓錐曲線的
通徑 , 物理學中又稱為
正焦弦 。
類似圓,與圓錐曲線交於兩點的直線上兩交點間的線段稱為
弦 ;過焦點的弦稱為
焦點弦 。
對於同一個橢圓或雙曲線,有兩個“焦點-準線”的組合可以得到它。因此,橢圓和雙曲線有兩個焦點和兩條準線。而拋物線只有一個焦點和一條準線。
圓錐曲線關於過焦點與準線垂直的直線對稱,在橢圓和雙曲線的情況,該直線通過兩個焦點,該直線稱為圓錐曲線的焦軸 。對於橢圓和雙曲線,還關於焦點連線的垂直平分線對稱。
Pappus定理 :圓錐曲線上一點的焦半徑長度等於該點到相應準線的距離乘以
離心率 。
Pascal定理 :圓錐曲線的內接六邊形,若對邊兩兩不平行,則該六邊形對邊延長線的交點
共線 。(對於退化的情形也適用)
Brianchon定理 :圓錐曲線的
外切 六邊形,其三條
對角線 共點。
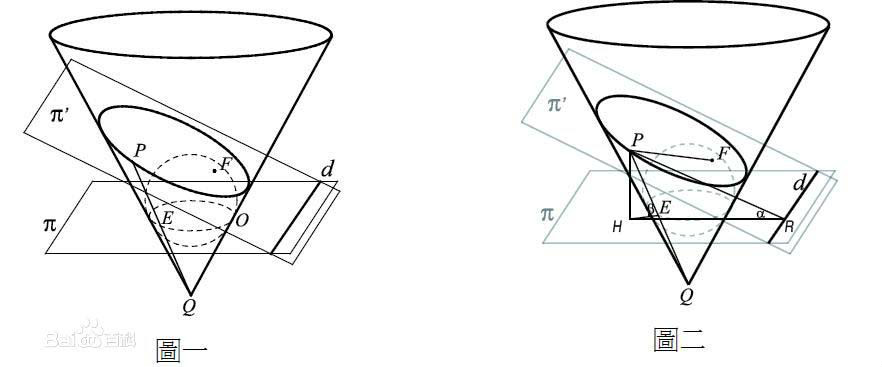
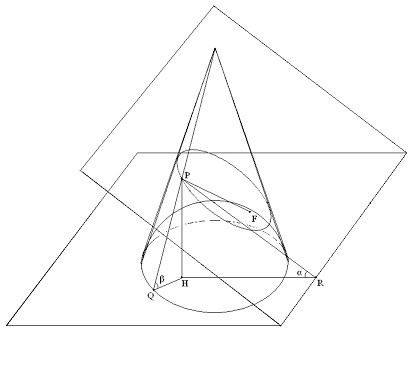
定理 由比利時數學家G.F.Dandelin 1822年得出的
冰淇淋定理 證明了圓錐曲線幾何定義與焦點-準線定義的等價性。
即有一以Q為頂點的圓錐(蛋筒),有一平面π'(你也可以說是餅乾)與其相截得到了圓錐曲線,作球與平面π'及圓錐相切,在曲線為橢圓或雙曲線時平面與球有兩個切點,拋物線只有一個(或者另一個在無窮遠處),則切點為焦點。又球與圓錐之交為圓,設以此圓所在平面π與π'之交為直線d(曲線為圓時d為無窮遠線),則d為準線。
圖只畫了橢圓,證明對拋物線雙曲線都適用,即證,任一個切點為焦點,d為準線。
證:假設P為曲線上一點,聯線PQ交圓O於E。設平面π′與π的交角為α,圓錐的母線(如PQ)與平面π的
交角 為β。設P到平面π 的垂足為H,H到直線d的
垂足 為R,則PR為P到d的
垂線 (
三垂線定理 ),而∠PRH=α。因為PE、PF同為
圓球 之
切線 ,得PE=PF。
如此則有:PR·sinα=PE·sinβ=PF·sinβ=PH
歷史 對於圓錐曲線的最早發現,眾說紛紜。有人說,古希臘數學家在求解“立方倍積”問題時,發現了圓錐曲線:設x、y為a和2a的
比例中項 ,即
,則
,
,
,從而求得
。又有人說,古希臘數學家在研究平面與圓錐面相截時發現了與“立方倍積”問題中一致的結果。還有認為,古代天文學家在製作
日晷 時發現了圓錐曲線。日晷是一個傾斜放置的圓盤,中央垂直於圓盤面立一桿。當太陽光照在日晷上,桿影的移動可以計時。而在不同緯度的地方,桿頂尖繪成不同的圓錐曲線。然而,日晷的發明在古代就已失傳。
在《圓錐曲線》中,阿波羅尼總結了前人(
柏拉圖學派 的梅內赫莫斯為解決倍立方體問題而發現了圓錐曲線)的工作,尤其是歐幾里得的工作,並對前人的成果進行去粗存精、歸納提煉並使之系統化的工作,在此基礎上,又提出許多自己的創見。全書8篇,共487個命題,將圓錐曲線的性質網羅殆盡,以致後代學者幾乎沒有插足的餘地達千餘年。
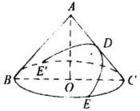
我們都知道,用一個平面去截一個雙圓錐面,會得到圓、橢圓、拋物線、雙曲線以及它們的退化形式:兩相交直線,一條直線和一個點,如圖1所示。
在此,我們僅介紹阿波羅尼關於圓錐曲線的定義。給定圓BC及其所在平面外一點A,則過A且沿圓周移動的一條直線生成一個雙錐面。
這個圓叫圓錐的底,A到圓心的直線叫圓錐的軸,軸未必垂直於底。
設錐的一個截面與底交於直線DE,取底圓的垂直於DE的一條直徑BC,於是含圓錐軸的△ABC叫軸三角形.軸三角形與圓錐曲線交於P、P’,PP’未必是圓錐曲線的軸,PP’M是由軸三角形與截面相交而定的直線,PM也未必垂直於DE。設QQ’是圓錐曲線平行於DE的弦,同樣QQ’被PP’平分,即VQ=QQ’。
現作AF∥PM,交BM於F,再在截面上作PL⊥PM。
對於橢圓、雙曲線,取L滿足,而拋物線,則滿足,對於橢圓、雙曲線有QV=PV·VR,對於拋物線有QV=PV·PL,這是可以證明的兩個結論。
在這兩個結論中,把QV稱為圓錐曲線的一個縱坐標線,那么其結論表明,縱坐標線的平方等於PL上作一個矩形的面積。對於橢圓來講,矩形PSRV尚未填滿矩形PLJV;而雙曲線的情形是VR>PL,矩形PSRV超出矩形PLJV;而拋物線,短形PLJV恰好填滿。故而,橢圓、雙曲線、拋物線的原名分別叫“虧曲線”、“超曲線”和“齊曲線”。這就是阿波羅尼引入的圓錐曲線的定義。
阿波羅尼所給出的兩個結論,也很容易用現代
數學符號 來表示:
趨向無窮大時,LS=0,即拋物線,亦即橢圓或雙曲線的
極限 形式。
在阿波羅尼的《圓錐曲線》問世後的13個世紀裡,整個數學界對圓錐曲線的研究一直沒有什麼新進展。11世紀,阿拉伯數學家曾利用圓錐曲線來解三次
代數方程 ,12世紀起,圓錐曲線經阿拉伯傳入歐洲,但當時對圓錐曲線的研究仍然沒有
突破 。直到16世紀,有兩件事促使了人們對圓錐曲線作進一步研究。一是德國天文學家
克卜勒 (
Kepler ,1571~1630)繼承了
哥白尼 的
日心說 ,揭示出行星按橢圓軌道環繞太陽運行的事實;二是義大利物理學家
伽利略 (
Galileo ,1564~1642)得出物體
斜拋運動 的軌道是
拋物線 。
人們發現圓錐曲線不僅是依附在圓錐面上的靜態曲線,而且是自然界物體運動的普遍形式。於是,對圓錐曲線的處理方法開始有了一些小變動。譬如,1579年
蒙蒂 (Guidobaldo del Monte,1545~1607)橢圓定義為:到兩個焦點距離之和為定長的動點的軌跡。從而改變了過去對圓錐曲線的定義。不過,這對圓錐曲線性質的研究推進並不大,也沒有提出更多新的定理或新的證明方法。
17世紀初,在當時關於一個數學對象能從一個形狀連續地變到另一形狀的新思想的影響下,克卜勒對圓錐曲線的性質作了新的闡述。他發現了圓錐曲線的焦點和離心率,並指出拋物線還有一個在無窮遠處的焦點,直線是
圓心 在無窮遠處的圓。從而他第一個掌握了這樣的事實:橢圓、拋物線、雙曲線、圓以及由兩條直線組成的退化圓錐曲線,都可以從其中一個連續地變為另一個,只須考慮焦點的各種移動方式。譬如,橢圓有兩個焦點F1、F2,如圖4,若左焦點F1固定,考慮F2的移動,當F2向左移動,橢圓逐漸趨向於圓,F1與F2重合時即為圓;當F2向右移動,橢圓逐漸趨向於拋物線,F2到無窮遠處時即為拋物線;當F2從無窮遠處由左邊回到圓錐曲線的軸上來,即為雙曲線;當F2繼續向右移動,F2又與F1重合時即為兩相交直線,亦即退化的圓錐曲線。這為圓錐曲線現代的統一定義提供了一個合乎邏輯的直觀基礎。
隨著
射影幾何 的創始,原本為畫家提供幫助的投射、截影的方法,可能由於它與
錐面 有著天然的聯繫,也被用於圓錐曲線的研究。在這方面法國的三位數學家
笛沙格 (Desargue1591-1661)、
帕斯卡 (Pascal,1623-1662)和拉伊爾(Phailippe de La Hire,1640~1718)得出了一些關於圓錐曲線的特殊的定理,可謂別開生面。而當法國另外兩位數學家笛卡兒和費馬創立了解析幾何,人們對圓錐曲線的認識進入了一個新階段,對圓錐曲線的
研究方法 既不同於
阿波羅尼 ,又不同於
投射 和截影法,而是朝著
解析法 的方向發展,即通過建立坐標系,得到圓錐曲線的
方程 ,進而利用方程來研究圓錐曲線,以期擺脫幾何直觀而達到抽象化的目標,也可求得對圓錐曲線研究高度的概括和統一。
到18世紀,人們廣泛地探討了解析幾何,除
直角坐標系 之外又建立
極坐標系 ,並能把這兩種坐標系相互轉換。在這種情況下表示圓錐曲線的
二次方程 也被化為幾種標準形式,或者引進曲線的
參數方程 。1745年歐拉發表了《分析引論》,這是解析幾何發展史上的一部重要著作,也是圓錐曲線研究的經典之作。在這部著作中,歐拉給出了現代形式下圓錐曲線的系統闡述,從一般二次方程出發,圓錐曲線的各種情形,經過適當的
坐標變換 ,總可以化以下標準形式之一:繼
歐拉 之後,三維解析幾何也蓬勃地發展起來,由圓錐曲線導出了許多重要的曲面,諸如圓柱面、橢球面、單葉和雙葉
雙曲面 以及各種
拋物面 等。
總而言之,圓錐曲線無論在數學以及其他科學技術領域,還是在我們的實際生活中都占有重要的地位,人們對它的研究也不斷深化,其研究成果又廣泛地得到套用。這正好反映了人們認識事物的目的和規律。
在此,要提到的是我國數學教師胡新平在2016年給出的新成果,千百年來,平面解析幾何的主要理論一直再無大的進展,即使焦點—準線系統統一性從公元300多年Pappus首次發現至今已1700年了,其存在的明顯不足也一直沒能得到完善。事實上,人們也一直在尋求以幾何方式統一七類二次曲線,而胡新平老師給出了包含一、二次曲線全部八類曲線的幾何統一形式,該統一是焦點-準線下統一性的推廣,也是僅見到的完備的、幾何形式的統一,這使得平面解析幾何向前邁出了里程碑的一步。也是我國數學工作者在平面解析幾何學科發展史上留下的深深印記。
性質 一、二次曲線的統一方程和性質可以參看《數學通報》2016,12期《一、二次曲線的軌跡統一及性質》一文。
橢圓
文字語言定義:平面內一個動點到一個
定點 與一條定
直線 的距離之比是一個小於1的正常數e。平面內一個動點到兩個定點(焦點)的距離和等於定長2a的點的
集合 (設動點為P,兩個定點為F1和F2,則PF1+PF2=2a)。定點是橢圓的焦點,定直線是橢圓的準線,常數e是橢圓的
離心率 。
雙曲線(的一支)
文字語言定義:平面內一個動點到一個定點與一條定直線的距離之比是一個大於1的常數e;平面內一個動點到兩個定點(焦點)的距離差等於定長2a的點的集合(設動點為P,兩個定點為F1和F2,則│PF1-PF2│=2a)定點是雙曲線的焦點,定直線是雙曲線的準線,常數e是雙曲線的
離心率 。
標準方程:
其中a>0,b>0,c2 =a2 +b2 .
其中a>0,b>0,c2 =a2 +b2 .
參數方程:x=asecθ;y=btanθ (θ為參數 )
拋物線
文字語言定義:平面內一個動點到一個定點與一條定直線的距離之比是等於1。定點是拋物線的
焦點 ,定直線是拋物線的
準線 。
x=2pt
2 y=2pt (t為參數) t=1/tanθ(tanθ為曲線上點與坐標原點確定
直線的斜率 )
特別地,t可等於0 y=ax2 +bx+c (開口方向為y軸,a≠0) x=ay2 +by+c (開口方向為x軸,a≠0 )
離心率
橢圓 ,
雙曲線 ,
拋物線 這些圓錐曲線有統一的定義:平面上,到定點的距離與到定直線的距離的比e是常數的點的軌跡叫做圓錐曲線。且當0<e<1時為橢圓:當e=1時為拋物線;當e>1時為
雙曲線 。
這裡的參數e就是圓錐曲線的離心率,它不僅可以描述圓錐曲線的類型,也可以描述圓錐曲線的具體形狀,簡言之,離心率相同的圓錐曲線都是相似圖形。一個圓錐曲線,只要確定了離心率,形狀就確定了。特別的,因為拋物線的離心率都等於1,所以所有的拋物線都是相似圖形。
極坐標方程
其中l表示半徑,e表示離心率;
2、在平面坐標系中,圓錐曲線極坐標方程可表示為:
焦半徑
圓錐曲線左右焦點為F1、F2,其上任意一點為P(x,y),則焦半徑為:
|PF1|=a+ex(PF1>PF2)
|PF2|=a-ex(PF2<PF1)
P在左支,|PF1|=-a-ex |PF2|=a-ex
P在右支,|PF1|=a+ex |PF2|=-a+ex
P在下支,|PF1|= -a-ey |PF2|=a-ey
P在上支,|PF1|= a+ey |PF2|=-a+ey
|PF|=x+p/2
切線方程
焦準距
圓錐曲線的焦點到準線的距離p,叫圓錐曲線的
焦準距 ,或
焦參數 。
拋物線:p
焦點三角形
橢圓或雙曲線上的一點與兩焦點所構成的三角形。
設F1 、F2 分別為橢圓或雙曲線的兩個焦點,P為橢圓或雙曲線上的一點且PF1 F2 能構成三角形。
通徑
對比
標準方程
x2 /a2 +y2 /b2 =1 (a>b>0)
x2 /a2 -y2 /b2 =1 (a>0,b>0)
y2 =2px (p>0)
範圍
x∈[-a,a]
x∈(-∞,-a]∪[a,+∞)
x∈[0,+∞)
關於x軸,y軸,原點對稱
關於x軸,y軸,原點對稱
關於x軸對稱
頂點
(a,0),(-a,0),(0,b),(0,-b)
(a,0),(-a,0)
(0,0)
(c,0),(-c,0)2 =a2 -b2 】
(c,0),(-c,0)2 =a2 +b2 】
(p/2,0)
x=±a2 /c
x=±a2 /c
x=-p/2
——————
y=±(b/a)x
—————
e=c/a,e∈(0,1)
e=c/a,e∈(1,+∞)
e=1
∣PF1 ∣=a+ex2 ∣=a-ex
∣PF1 ∣=∣ex+a∣2 ∣=∣ex-a∣
∣PF∣=x+p/2
p=b2 /c
p=b2 /c
p
2b2 /a
2b2 /a
2p
x=a·cosθ
x=a·secθ
x=2pt2
x0·x/a2 +y0·y/b2 =1
x0x/a2 -y0·y/b2 =1
y0·y=p(x+x0)
y=kx±√(a2 ·k2 +b2 )
y=kx±√(a2 ·k2 -b2 )
y=kx+p/2k
中點弦問題
已知圓錐曲線內一點為圓錐曲線的一弦中點,求該弦的方程:
設出弦的兩端點坐標(x
1 ,y
1 )和(x
2 ,y
2 ),代入圓錐曲線的方程,將得到的兩個方程相減,運用
平方差公式 得[(x
1 +x
2 )(x
1 -x
2 )]/a
2 +[(y
1 +y
2 )(y
1 -y
2 )/b
2 ]=0
由
斜率 為(y
1 -y
2 )/(x
1 -x
2 ),可以得到斜率的取值(使用時注意
判別式 的問題)
統一方程
平面直角坐標系內的任意圓錐曲線可用如下方程表示:
其中,α∈[0,2π),p>0,e≥0。
①e=1時,表示以F(g,h)為焦點,p為焦點到
準線 距離的
拋物線 。其中
與極軸夾角α(A為拋物線頂點)。
②0<e<1時,表示以F
1 (g,h)為一個焦點,p為焦點到
準線 距離,e為離心率的
橢圓 。其中
與極軸夾角α。
③e>1時,表示以F
2 (g,h)為一個焦點,p為焦點到
準線 距離,e為離心率的
雙曲線 。其中
與極軸夾角α。
④e=0時,表示點F(g,h)。
五點法求平面內圓錐曲線可以採用該統一方程。代入五組有序實數對,求出對應參數。
註:此方程不適用於圓錐曲線的其他退化形式,如
圓 等。
判別法 δ>0
Δ=0
δ>0
Δ≠0
ΔS<0
δ>0
Δ≠0
ΔS>0
虛橢圓
δ<0
Δ=0
δ<0
Δ≠0
δ=0
Δ≠0
δ=0
Δ=0
D2 +E2 -AF-CF<0
平行直線
δ=0
Δ=0
D2 +E2 -AF-CF=0
重合直線
δ=0
Δ=0
D2 +E2 -AF-CF>0
定理介紹 CGY-EH定理(又稱
圓錐曲線硬解定理 )是一套求解橢圓\雙曲線與直線相交時∆、 x1+x2 、x1* x2、y1+y2、y1*y2 及相交弦長的
簡便 算法.
定理內容 若曲線
與直線Aχ+By+C=0相交於E、F兩點,則:
定理說明 套用於雙曲線
時,應將
代入,同時
不應為零,即ε不為零。
求解y1+y2與 y1*y2隻須將A與B的值互換且m與n的值互換.可知ε與∆'的值不會因此而改變。
定理補充 聯立曲線方程與y=kx+
是現行高考中比聯立”Ax+By+C=0“更為普遍的現象。其中聯立後的二次方程是標準答案中必不可少的一項,x1+x2,x1x2都可以直接通過該方程與韋達定理求得,唯獨弦長的表達式需要大量計算。這裡給出一個CGY-EH的斜率式簡化公式,以減少記憶量,以便在考試中套用。
這裡的
既可以是常數,也可以是關於k的代數式。由這個公式我們可以推出:
由於在高考中CGY-EH定理不可以直接套用,所以學生如此解答才可得全步驟分(省略號的內容需要考生自己填寫):
聯立兩方程得……(二次式子)(*)
所以x1+x2=……①,x1x2=……②;
所以|x1-x2|=√(x1+x2)^2-4x1x2=……(此時代入①、②式得到一個大式子,但不必化簡)
化簡得|x1-x2|=
(偷偷地直接套公式,不必真化簡)
定理簡證 設曲線x^2/m+y^2/n=1①與直線 Aχ+By+C=0②相交於E、F兩點,聯立①②式可得最終的二次方程:
(A^2 m+B^2 n) x^2+2ACmx+C^2 m-mnB^2=0
x_1+x_2=(-2ACm)/(A^2 m+B^2 n)
x_1 x_2=(m(C^2-B^2 n))/(A^2 m+B^2 n)
∆=4mnB^2 (ε-C^2)
對於
等價 的一元二次方程∆的數值不唯一,且 ∆的意義僅在於其與零的關係,故由4B^2>0恆成立,則可取與∆同號的∆'=mn(ε-C^2)作為∆的值。
由|EF|=√(〖(x_1-x_2)〗^2+〖(y_1-y_2)〗^2 )=√((1+A^2/B^2 )[〖(x_1+x_2)〗^2-4x_1 x_2 ] )
可得|EF|=√((A^2+B^2)4mn(A^2 m+B^2 n-C^2))/(|A^2 m+B^2 n|)
令ε=A^2 m+B^2 n 則得到CGY-EH定理:
x_1+x_2=(-2ACm)/ε ; x_1 x_2=(m(C^2-B^2 n))/ε ; ∆'=mn(ε-C^2) ; |EF|=(2√((A^2+B^2)∆'))/(|ε|)
漫談 圓錐曲線包括橢圓、拋物線、雙曲線和圓,通過直角坐標系,它們又與二次方程對應,所以,圓錐曲線又叫做
二次曲線 。圓錐曲線一直是幾何學研究的重要課題之一,在我們的實際生活中也存在著許許多多的圓錐曲線。
我們生活的地球每時每刻都在環繞太陽的橢圓軌跡上運行,太陽系其他行星也如此,太陽則位於橢圓的一個
焦點 上。如果這些行星運行速度增大到某種程度,它們就會沿拋物線或雙曲線運行。人類發射人造地球衛星或人造行星就要遵照這個原理。相對於一個物體,按
萬有引力定律 受它吸引的另一物體的運動,不可能有任何其他的軌道了。因而,圓錐曲線在這種意義上講,它構成了我們宇宙的基本形式。
由拋物線繞其軸旋轉,可得到一個叫做旋轉物面的曲面。它也有一條軸,即拋物線的軸。在這個軸上有一個具有奇妙性質的焦點,任何一條過焦點的直線由
拋物面 反射出來以後,都成為平行於軸的直線。這就是我們為什麼要把探照燈反光鏡做成旋轉拋物面的道理。由雙曲線繞其虛軸旋轉,可以得到
單葉雙曲面 ,它又是一種直紋曲面,由兩組母直線族組成,各組內母直線互不相交,而與另一組母直線卻相交。人們在設計高大的立塔(如
冷卻塔 )時,就採取單葉雙曲面的體形,既輕巧又堅固。
由此可見,對於圓錐曲線的價值,無論如何也不會估計過高。
光學性質 橢圓 從橢圓一個焦點發出的光,經過橢圓反射後,
反射光線 都匯聚到橢圓的另一個
焦點 上。
雙曲線 從雙曲線一個焦點發出的光,經過雙曲線
反射 後,反射光線的反向延長線都匯聚到雙曲線的另一個焦點上。
拋物線 從拋物線的焦點發出的光,經過拋物線反射後,反射光線都平行於拋物線的對稱軸。
一束
平行光 垂直於拋物線的準線,向拋物線的開口射進來,經拋物線反射後,反射光線匯聚在拋物線的焦點。
套用 如圖所示為圓錐曲線中橢圓的套用——回聲山谷。在西方某些橢圓
穹頂 的大教堂里也有這種現象。
橢圓的聲學性質 圓錐截面在天文學中是重要的:根據牛頓萬有引力定律相互作用的兩個巨大物體的軌道是圓錐截面,如果它們的共同質心被認為是靜止的。如果它們綁定在一起,它們將跟蹤橢圓;如果他們分開,他們將會跟隨拋物線或雙曲線。看到兩體問題。
對於古生物學中的某些化石,了解圓錐截面可以幫助了解某些生物體的三維形狀。
圓錐截面的反射特性用於探照燈,射電望遠鏡和一些光學望遠鏡的設計。使用拋物面鏡作為反射器,在探照燈下使用焦點上的燈泡。在加那利群島拉帕爾馬的4.2米赫歇爾光學望遠鏡使用主要的拋物面鏡將光反射到次級雙曲面鏡,這反映了它再次成為第一鏡後面的焦點。

 圖片3
圖片3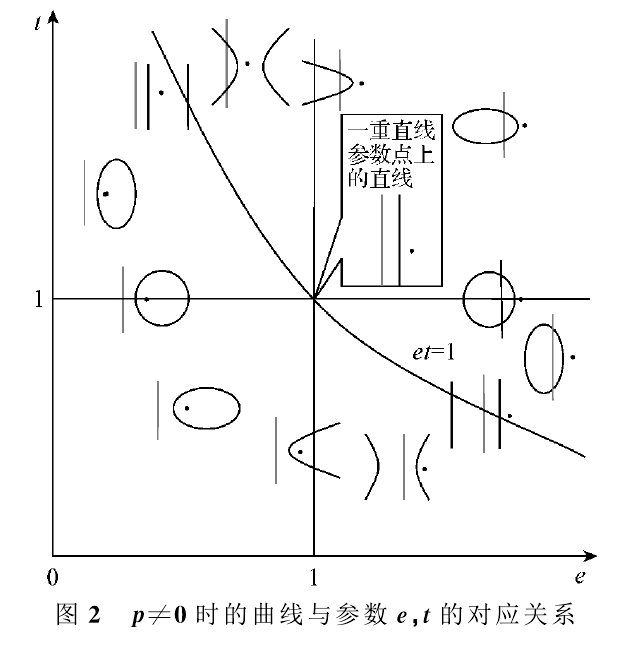 圖1
圖1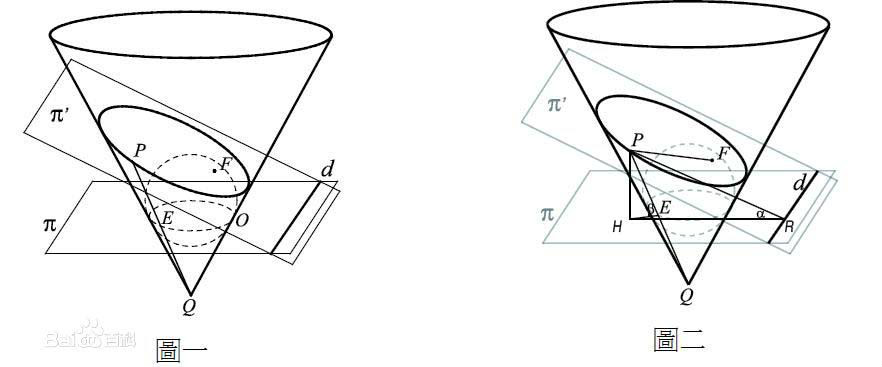



















































 橢圓的聲學性質
橢圓的聲學性質