簡介
在數學中,拋物線是一個平面曲線,它是鏡像對稱的,並且當定向大致為U形(如果不同的方向,它仍然是拋物線)。它適用於幾個表面上不同的數學描述中的任何一個,這些描述都可以被證明是完全相同的曲線。
拋物線的一個描述涉及一個點(焦點)和一條線(該線)。焦點並不在於準則。拋物線是該平面中與準線和焦點等距的點的軌跡。拋物線的另一個描述是作為圓錐截面,由右圓錐形表面和平行於與錐形表面相切的另一平面的平面的交點形成。第三個描述是代數。
垂直於準線並通過焦點的線(即通過中間分解拋物線的線)被稱為“對稱軸”。與對稱軸相交的拋物線上的點被稱為“頂點”,並且是拋物線最鋒利彎曲的點。沿著對稱軸測量的頂點和焦點之間的距離是“焦距”。 “直腸直腸”是拋物線的平行線,並通過焦點。拋物線可以向上,向下,向左,向右或向另一個任意方向打開。任何拋物線都可以重新定位並重新定位,以適應任何其他拋物線 - 也就是說,所有拋物線都是幾何相似的。
拋物線具有這樣的性質,如果它們由反射光的材料製成,則平行於拋物線的對稱軸行進並撞擊其凹面的光被反射到其焦點,而不管拋物線在哪裡發生反射。相反,從焦點處的點源產生的光被反射成平行(“準直”)光束,使拋物線平行於對稱軸。聲音和其他形式的能量也會產生相同的效果。這種反射性質是拋物線的許多實際套用的基礎。
拋物線具有許多重要的套用,從拋物面天線或拋物線麥克風到汽車前照燈反射器到設計彈道飛彈。它們經常用於物理,工程和許多其他領域。
發展歷程
Apollonius 所著的八冊《
圓錐曲線》(Conics)集其大成,可以說是
古希臘解析幾何學一個
登峰造極的精擘之作。今日大家熟知的 ellipse(
橢圓)、parabola(拋物線)、hyperbola(
雙曲線)這些名詞,都是 Apollonius 所發明的。當時對於這種既簡樸又完美的曲線的研究,乃是純粹從
幾何學的觀點,研討和圓密切相關的這種曲線;它們的幾何乃是圓的幾何的自然推廣,在當年這是一種純理念的探索,並不寄望也無從預期它們會真的在大自然的基本結構中扮演著重要的角色。
 拋物線問題
拋物線問題標準方程
定義
特點
在拋物線
中,焦點是
,準線的
方程是
,離心率
,範圍:
;
在拋物線
中,焦點是
,準線的
方程是
,離心率
,範圍:
;
在拋物線
中,焦點是
,準線的方程是
,離心率
,範圍:
;
在拋物線
中,焦點是
,準線的方程是
,離心率
,範圍:
。
 拋物線
拋物線四種方程
拋物線四種方程的異同
共同點:
不同點:
①對稱軸為x軸時,方程右端為±2px,方程的左端為y^2;對稱軸為y軸時,方程的右端為±2py,方程的左端為x^2;
②開口方向與x軸(或y軸)的
正半軸相同時,焦點在x軸(y軸)的正半軸上,方程的右端取
正號;開口方向與x(或y軸)的
負半軸相同時,焦點在x軸(或y軸)的負半軸上,方程的右端取
負號。
切線方程
拋物線y
1=2px上一點(x0,y0)處的切線方程為:
。
拋物線y1=2px上過焦點斜率為k的方程為:y=k(x-p/2)。
相關參數
(對於向右開口的拋物線y1=2px)
離心率:e=1(恆為定值,為拋物線上一點與準線的距離以及該點與焦點的距離比)
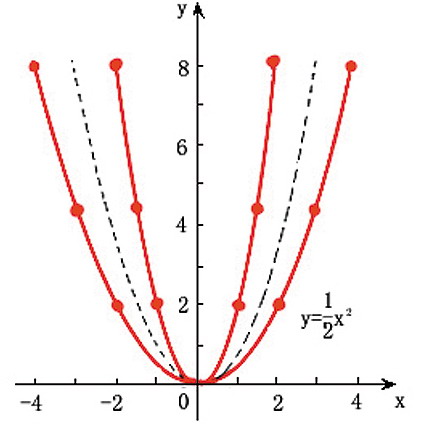 二次函式的圖像是一條拋物線
二次函式的圖像是一條拋物線 通徑:2P ;定義:
圓錐曲線(除圓外)中,過焦點並垂直於軸的弦
定義域:對於拋物線y
1=2px,p>0時,定義域為x≥0,p<0時,定義域為x≤0;對於拋物線x
1=2py,定義域為R。
值域:對於拋物線y
1=2px,值域為R,對於拋物線x
1=2py,p>0時,值域為y≥0,p<0時,值域為y≤0。
術語解釋
準線、焦點:拋物線是平面內到一定點和到一條不過此點的定直線的距離相等的點的軌跡。這一定點叫做拋物線的焦點,定直線叫做拋物線的準線。
直徑:拋物線的直徑是拋物線一組平行弦中點的軌跡。這條直徑也叫這組平行弦的
共軛直徑。
主要直徑:拋物線的主要直徑是拋物線的軸。
拋物線即把物體拋擲出去,落在遠處地面,這物體在空中經過的曲線。
解析式求法
以焦點在X軸上為例
知道P(x0,y0)
令所求為y1=2px
則有y01=2px0
故2p=y01/x0
故拋物線為y1=(y01/x0)x
現總結如下:
(1)知道拋物線過三個點(x1,y1)(x2,y2)(x3,y3)設拋物線方程為y=ax2+bx+c,
將各個點的坐標代進去得到一個三元一次方程組,解得a,b,c的值即得解析式。
(2)知道拋物線的與x軸的兩個交點(x1,0),(x2,0),並知道拋物線過某一個點(m,n),
設拋物線的方程為y=a(x-x1)(x-x2),然後將點(m,n)代入去求得二次項係數a。
(3)知道對稱軸x=k,
設拋物線方程是y=a(x-k)2+b,再結合其它條件確定a,c的值。
(4)知道二次函式的最值為p,
設拋物線方程是y=a(x-k)2+p,a,k要根據其它條件確定。
光學性質
經焦點的
光線經拋物線
反射後的光線平行於拋物線的對稱軸。各種
探照燈、汽車燈即利用拋物線(面)的這個性質,讓
光源處在焦點處以發射出(準)
平行光。
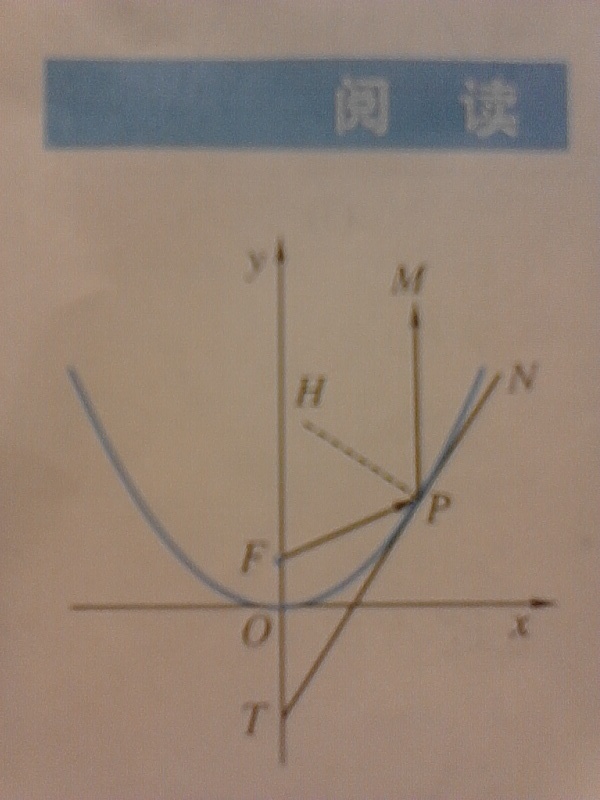
證明:設P(x0,y0),PT是拋物線在P處的切線,PH⊥PT,拋物線的方程為
(a>0),焦點F坐標為(0,
)。
所以切線PN的斜率為2ax0,方程為y-y0=2ax0(x-x0)
所以PF=FT,∠FTP=∠FPT,
又∠FPT=∠MPN
所以∠FTP=∠MPN
MP平行於y軸。
 光學性質
光學性質擴展公式
拋物線:y = ax1 + bx + c (a≠0)
就是y等於ax 的平方加上 bx再加上 c;
a > 0時開口向上;
a < 0時開口向下;
c = 0時拋物線經過原點;
b = 0時拋物線對稱軸為y軸。
h是頂點坐標的x;
k是頂點坐標的y;
一般用於求最大值與最小值。
拋物線標準方程:y1=2px
它表示拋物線的焦點在x的正半軸上,焦點坐標為(p/2,0) 準線方程為x=-p/2。
由於拋物線的焦點可在任意半軸,故共有標準方程y1=2px,y1=-2px,x1=2py,x1=-2py。
二次函式圖象
在
平面直角坐標系中作出二次函式y=ax
1+bx+c的圖像,可以看出,在沒有特定定義域的二次函式圖像是一條永無止境的拋物線。 如果所畫圖形準確無誤,那么二次函式圖像將是由
平移得到的。
對稱軸與
二次函式圖像
唯一的交點為二次函式圖象的頂點P。
特別地,當b=0時,二次函式圖像的對稱軸是y軸(即直線x=0),是頂點的橫坐標(即x=?)。
a,b異號,對稱軸在y軸右側
二次函式圖像有一個頂點P,坐標為P(h,k)。
當h=0時,P在y軸上;當k=0時,P在x軸上。即可表示為頂點式y=a(x-h)1+k(a≠0)
當a>0時,二次函式圖象向上開口;當a<0時,拋物線向下開口。
|a|越大,則二次函式圖像的開口越小。
一次項係數b和二次項係數a共同決定對稱軸的位置。
當a>0,與b同號時(即ab>0),對稱軸在y軸左; 因為對稱軸在左邊則對稱軸小於0,也就是- b/2a<0,所以 b/2a要大於0,所以a、b要同號。
當a>0,與b異號時(即ab<0),對稱軸在y軸右。因為對稱軸在右邊則對稱軸要大於0,也就是- b/2a>0, 所以b/2a要小於0,所以a、b要異號。
可簡單記憶為左同右異,即當a與b同號時(即ab>0),對稱軸在y軸左;當a與b異號時(即ab<0 ),對稱軸在y軸右。
事實上,b有其自身的幾何意義:二次函式圖象與y軸的交點處的該二次函式圖像
切線的函式解析式(
一次函式)的斜率k的值。可通過對二次函式
求導得到。
 二次函式圖像
二次函式圖像相關結論
A(x1,y1),B(x2,y2),A,B在拋物線y1=2px上,則有:
① 直線AB過焦點時,x1x2 = p2/4 , y1y2 = -p2;
(當A,B在拋物線x2=2py上時,則有x1x2 = -p2 , y1y2 = p2/4 , 要在直線過焦點時才能成立)
② 焦點弦長:|AB| = x1+x2+P = 2P/[(sinθ)1]=(x1+x2)/2+P;
③ (1/|FA|)+(1/|FB|)= 2/P;(其中長的一條長度為P/(1-cosθ),短的一條長度為P/(1+cosθ))
④若OA垂直OB則AB過定點M(2P,0);
⑤
焦半徑:|FP|=x+p/2 (拋物線上一點P到焦點F的距離等於P到準線L的距離);
⑥
弦長公式:AB=√(1+k
1)*│x
1-x
2│;
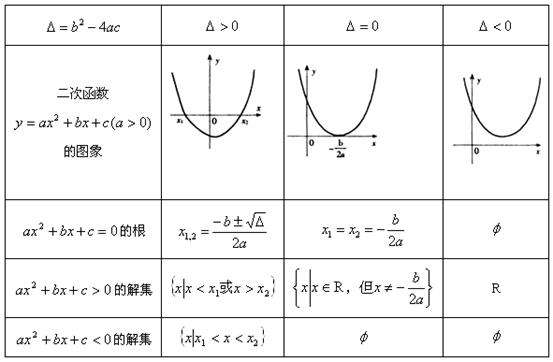
⑦△=b1-4ac;
⑵△=b1-4ac=0有兩個一樣的實數根;
⑶△=b1-4ac<0沒實數根。
⑧由拋物線焦點到其切線的垂線的距離是焦點到切點的距離與到頂點距離的
比例中項;
⑨標準形式的拋物線在(x0,y0 )點的切線是:yy0=p(x+x0)
(注:圓錐曲線切線方程中x2=x*x0 , y2 =y*y0 , x=(x+x0)/2 , y=(y+y0)/2 )
 拋物線問題
拋物線問題










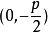



 拋物線
拋物線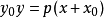
 二次函式的圖像是一條拋物線
二次函式的圖像是一條拋物線

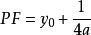



 光學性質
光學性質



 二次函式圖像
二次函式圖像