基本介紹
- 中文名:對稱軸
- 外文名:axis of symmetry
- 所屬學科:幾何學
- 定義:使圖形成軸對稱或旋轉對稱的直線
- 舉例:正方形、圓、拋物線、雙曲線等
定義,定義一,定義二,定理,常見軸對稱圖形,
定義
定義一
在平面上,如果圖形F的所有點關於平面上的直線 成軸對稱,直線
成軸對稱,直線 叫做圖形下的對稱軸。
叫做圖形下的對稱軸。


定義二
圖1中的三個圖形分別有兩條、一條、四條對稱軸。
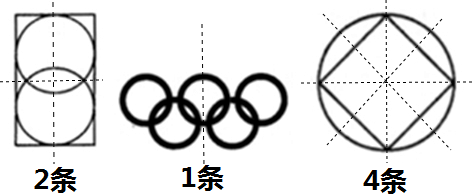 圖1
圖1定理
①對稱軸上的任意一點與對稱點的距離耝等;
②對稱點所連線段被對稱軸垂直平分。
推論:兩個圖形如果關於某直線軸對稱,那么這兩個圖形是全等圖形。
常見軸對稱圖形
幾種常見的軸對稱圖形和中心對稱圖形:
對稱軸的條數:角有一條對稱軸,即該角的角平分線;等腰三角形有一條對稱軸,是底邊的垂直平分線;等邊三角形有三條對稱軸,分別是三邊上的垂直平分線;菱形有兩條對稱軸,分別是兩條對角線所在的直線,矩形有兩條對稱軸分別是兩組對邊中點的直線;
中心對稱圖形:線段 、平行四邊形、菱形、矩形、正方形、圓等。
對稱中心:線段的對稱中心是線段的中點;平行四邊形、菱形、矩形、正方形的對稱中心是對角線的交點;圓的對稱中心是圓心。
說明:線段、菱形、矩形、正方形以及圓它們即是軸對稱圖形又是中心對稱圖形。
坐標系中的軸對稱變換與中心對稱變換: